Ноябрь

Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Даны векторы \(\vec{a}(2;-5)\) и \(\vec{b}(5;7)\). Найдите скалярное произведение векторов \(0{,}6\vec{a}\) и \(1{,}4\vec{b}\)

В цилиндрический сосуд налили 1800 см³ воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объём детали? Ответ выразите в см³.

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.

Вероятность того, что на тестировании по истории учащийся Т. верно решит больше 7 задач, равна 0,71. Вероятность того, что Т. верно решит больше 6 задач, равна 0,78. Найдите вероятность того, что Т. верно решит ровно 7 задач.

Найдите корень уравнения \(4^{x-2}=\left(\dfrac12\right)^{3x+1}\)

Вычислите \(\dfrac{\log_{17}169}{\log_{17}13}\)

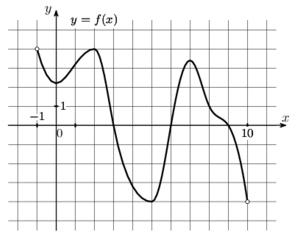
На рисунке изображён график функции \( y = f (x) \), определённой на интервале \( (−1;10) \). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

Катер должен пересечь реку шириной \(L = 100\) м и со скоростью течения \(u =0{,}5\) м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением \(t=\dfrac{L}{u}\mathrm{ctg\,}\alpha\), где \(\alpha\) − острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом \(\alpha\) (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?

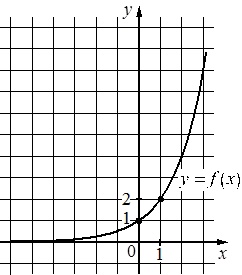
На рисунке изображен график функции вида \(f(x)=a^x\). Найдите \(f(4)\)

​

Найдите наименьшее значение функции \(y=5x-\ln(5x)+10\) на отрезке \(\left[ \dfrac2{15};\dfrac7{15}\right]\).