Задачи ЕГЭ база
На прямой отмечены точки P , Q, R и S.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| P | 1) \(\log_{2}{10}\) |
| Q | 2) \(\dfrac{7}{3}\) |
| R | 3) \(\sqrt{26}\) |
| S | 4) \(0{,}6^{-1}\) |
Запишите в ответ цифры в порядке, соответствующем буквам PQRS.
На прямой отмечены точки A,B,C и D
Установите соответствие межлу указанными точками и и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) \(\log_{4}{0{,}5}\) |
| B | 2) \(\dfrac{50}{11}\) |
| C | 3) \(0{,}6^{-2}\) |
| D | 4) \(\sqrt{0{,}68}\) |
Запишите в ответ цифры в порядке, соответствующем буквам ABCD без пробелов и дополнительных символов.
На координатной прямой отмечены число \(m\) и точки A, B, C, D.
Каждой точке соответствует одноиз чисел в правом столбце. Установите соответствие между указанными точками и числами. В ответ запишите цифры в порядке, соответствующем буквам ABCD.
| ТОЧКИ | ЧИСЛА |
| A | 1. \(-\dfrac2{m}\) |
| B | 2. \(6-m\) |
| C | 3. \(m-1\) |
| D | 4. \(m^2\) |
На координатной прямой отмечено 4 точки. Установите соответствие между точками и числовыми значениями.
| А) \(K\) | 1) \(\log_{3}{0{,}1}\) |
| Б) \(L\) | 2) \(\sqrt{7}\) |
| В) \(M\) | 3) \(\sin{70°}\) |
| Г) \(N\) | 4) \(3^{1{,}5}\) |
Каждому из четырёх неравенств слева соответствует одно из решений справа. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) \(2^{-x+1}<0{,}5\) | 1) \((4;+\infty)\) |
| Б) \(\dfrac{(x-2)^{2}}{x-4}<0\) | 2) \((2;4)\) |
| В) \(\log_{4}{x}>1\) | 3) \((2;+\infty)\) |
| Г) \((x-4)(x-2)<0\) | 4) \((-\infty;2)\cup(2;4)\) |
Запишите в ответ цифры в порядке, соответствующем буквам АБВГ без пробелов и дополнительных символов.
На прямой отмечены числа m и n.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами левого столбца и отрезками из правого столбца. В ответ запишите цифры, в порядке соответствующем буквам ABCD.
| ЧИСЛА | ОТРЕЗКИ |
| A) \(\dfrac1{n}+m\) | 1) [-4;-3] |
| B) \(mn\) | 2) [-1;0] |
| C) \(n^2-m^2\) | 3) [2;3] |
| D) 2(m+n) | 4) [4;5] |
На координатной прямой точками отмечены числа a, b, c, d и m. Установите соответствие между указанными точками и числами из правого столбца.
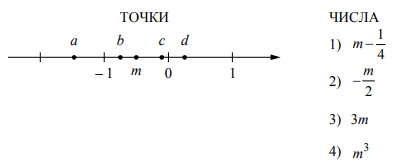
В ответ запишите цифры в порядке, соответствующем буквам \(abcd\).
Каждому из четырёх неравенств слева соответствует одно из решений, изображённых на координатной прямой справа. Установите соответствие между неравенствами и их решениями.
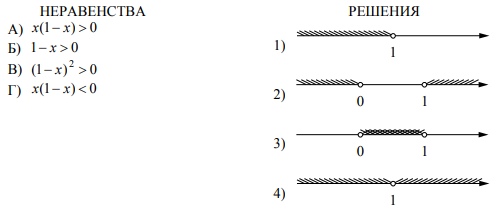
В ответ запишите цифры в порядке, соответствующем буквам АБВГ.
На прямой отмечены числа m и n.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами левого столбца и отрезками из правого столбца.
| ЧИСЛА | ОТРЕЗКИ |
| A) \(\dfrac{1}{n}+m\) | 1) [-4;-3] |
| Б) \(mn\) | 2) [-1;0] |
| В) \(n^{2}-m^{2}\) | 3) [2;3] |
| Г) \(2(m+n)\) | 4) [4;5] |
Поставьте в соответствие каждому неравенству множество его решений.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
|---|---|
| А) \(9 - x^2 \leqslant 0\) | 1) \((- 3; 3)\) |
| Б) \(9 - x^2 \geqslant 0\) | 2) \(( - \infty; - 3] \cup [3; + \infty)\) |
| В) \(\dfrac{1}{9 - x^2} < 0 \) | 3)\(( - \infty; - 3) \cup (3; + \infty)\) |
| Г)\(\dfrac{1}{9 - x^2} > 0 \) | 4) \([- 3; 3]\) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.