Задачи ОГЭ
- 1. Практическая задача I
- 2. Практическая задача II
- 3. Практическая задача III
- 4. Практическая задача IV
- 5. Практическая задача V
- 6. Вычисления
- 7. Координатная прямая. Числовые неравенства
- 8. Действительные числа. Степени. Сравнения
- 9. Уравнения
- 10. Теория вероятностей
- 11. Функции и графики
- 12. Расчеты по формулам
- 13. Неравенства
- 14. Прогрессии
- 15. Треугольники
- 16. Окружности
- 17. Четырехугольники и многоугольники
- 18. Фигуры на квадратной решетке
- 19. Анализ геометрических утверждений
- 20. Уравнения, выражения, неравенства
- 21. Сложные текстовые задачи
- 22. Построение графиков
- 23. Геометрические задачи на вычисление
- 24. Геометрические задачи на доказательство
- 25. Сложные геометрические задачи
2. Практическая задача II (Задачи ОГЭ)
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |

Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?

На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м × 1м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой. К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником \(BCC_1B_1\), где точки \(B\), \(O\) и \(C\) делят отрезок \(AD\) на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.

Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Справа от входа в квартиру располагаются кухня и санузел, причём площадь кухни больше площади санузла. Остальные два помещения — это спальня и гостиная. Гостиная имеет наибольшую площадь из всех помещений этой квартиры. Балкон и лоджия отсутствуют.

Из трёх окон квартиры одно шире двух других. Найдите ширину этого окна. Ответ дайте в сантиметрах.
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.

Вячеслав страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Чему равен КБМ на начало третьего года страхования?
Для маркировки автомобильных шин применяется единая система обозначений (см. рис. 1).

Первое число означает ширину \(В\) шины (ширину протектора) в миллиметрах (см. рис. 2). Второе число — отношение высоты боковины \(H\) к ширине шины \(B\) в процентах. Последующая буква указывает конструкцию шины. Например, буква \(R\) означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр \(d\) внутреннего отверстия в шине. Таким образом, общий диаметр колеса \(D\) легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие.

На сколько миллиметров радиус колеса с маркировкой \(195/60\, R14\) больше, чем радиус колеса с маркировкой \(165/70\, R14\)?

На плане изображено домохозяйство (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится сарай, а справа — гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2м ×0,1м и отмеченная на плане цифрой 6.
Тротуарная плитка продаётся в упаковках по 40 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
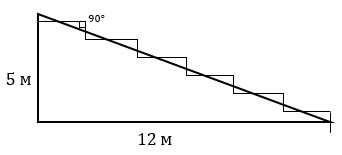
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 30 м, а верхняя точка находится на высоте 5 м от подножия.

Земледелец решил устроить террасы на своем участке (см. рисунок ниже), чтобы выращивать рис, пшено и кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла склона α, умноженный на 100%). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц \(a\). Оно оказалось равно 38 см. Высота купола зонта \(h\) (рис. 2) оказалась равна 25 см, а расстояние \(d\) между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
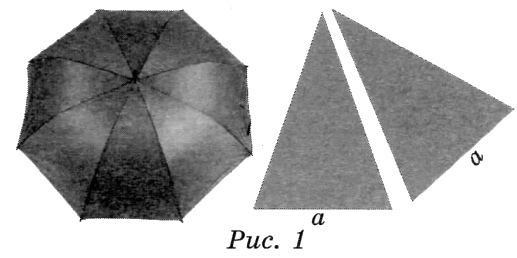
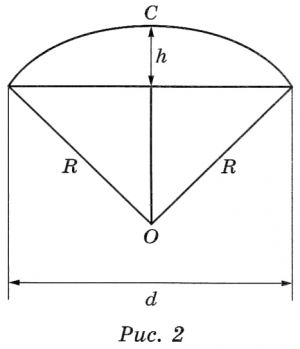
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.