На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-11;11). Найдите количество точек экстремума функции \(f(x)\), принадлежащих отрезку [-10;10].
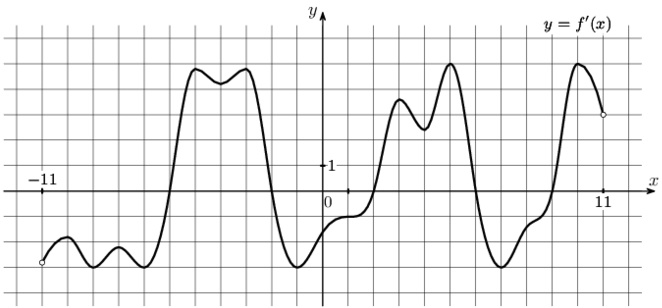

На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-11;11). Найдите количество точек экстремума функции \(f(x)\), принадлежащих отрезку [-10;10].

разве в этой задаче ответ 11 неверный?

благодарю, невнимательно прочитала условие

Нет-нет. Тебе дан график производной. Точки экстремума производной - это точки её пересечения с осью Х.

Правильный ответ 5, т.к. изображен график производной.


11 находится за пределами данного отрезка , прочитайте ещё раз условие

Ответ 5
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0
