На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
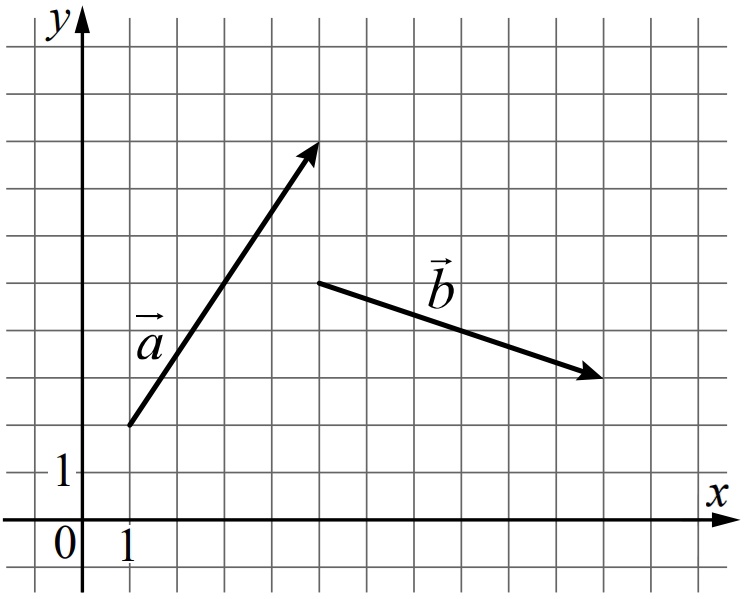

На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Вектор \(\vec{a}\): начало (1;2), конец (5;8).
Вектор \(\vec{b}\): начало (5;5), конец (11;3).
Координаты вектора равны разности координат его конца и начала:
\(\vec{a}\,\{5-1;8-2\}=\vec{a}\,\{4;6\}\)
\(\vec{b}\,\{11-5;3-5\}=\vec{b}\,\{6;-2\}\)
Скалярное произведение векторов равно сумме произведений их соответствующих координат:
\(\vec{a}\,\{x_1;y_1\}\), \(\vec{b}\,\{x_2;y_2\}\)
\(\vec{a}\cdot\vec{b}=x_1\cdot x_2+y_1\cdot y_2\)
В нашем случае:
\(\vec{a}\cdot\vec{b}=4\cdot6+6\cdot(-2)=24-12=12\)
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0