На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите \(\cos\alpha\), где \(\alpha\) - угол между векторами \(\vec{a}\) и \(\vec{b}\)
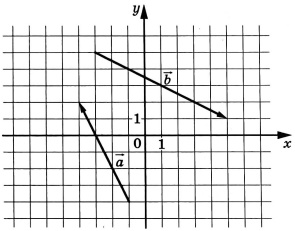

На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите \(\cos\alpha\), где \(\alpha\) - угол между векторами \(\vec{a}\) и \(\vec{b}\)

Как решать

Первым делом находишь координаты этих векторов. Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала вектора. Таким образом, у тебя получаются координаты двух векторов. Потом подставляешь в формулу и решаешь cos = (a * b)/(|a|*|b|). В числителе скалярное произведение, а в знаменателе произведение длин двух векторов(чтобы найди длину вектора, возводишь иксик в квадрат и игрик в квадрат, потом их складываешь и выносишь из-под корня).
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0