На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\) с целочисленными координатами. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
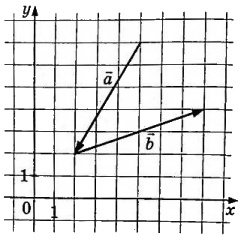

На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\) с целочисленными координатами. Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

a=AB(−3;−5)
b=BC(6;2)
-3*6=-18
что не так?

просят найти скалярное произведение, недостаточно просто перемножить x
a*b = x1*x2 + y1*y2 = | a | + | b | * cos a

Координаты вектора а = (-3;-5)
Координаты вектора b = (6;2)
Скалярное произведение= (-3*6)+(-5*2)=-28

Скалярное произведение это сумма произведений соответствующих координат, забыли умножить -5 на 2, ИТОГ -28

Мы умножаем -3 на 6 и складываем с умножением 2 на -5. И получаем ответ -28. Вроде бы так

Скалярное произведение находиться по формуле a*b= x1*x2+y1*y2, то есть -3*6+(-5)*2

А(-3;-5)
В(6;2)
Формула сколяр произведения х1•х2+у1•у2
-3•6+(-5)•2=-28
-3*6-5*2=-28

Решено не до конца. Если находим скалярное произведение, то -3*6+(-5)*2=-18-10=-28

а*b=-3*6+2*(-5)=-28

-3*6+(-5)*2=-18-10=-28
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0