Объем куба \(ABCDA_1B_1C_1D_1\) равен 48. Найдите объем многогранника \(AD_1B_1KML\), где \(K\), \(M\) и \(L\) – середины ребер \(AA_1\), \(A_1D_1\) и \(A_1B_1\) соответственно.
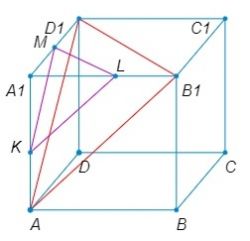
Объем куба \(ABCDA_1B_1C_1D_1\) равен 48. Найдите объем многогранника \(AD_1B_1KML\), где \(K\), \(M\) и \(L\) – середины ребер \(AA_1\), \(A_1D_1\) и \(A_1B_1\) соответственно.

Даже если брать этьо суждения из расписаной формулы площади треугольника, то там уже изначально а взята как высота.

Во-первых, высота не треугольника, а пирамиды. Речь про пирамиду \(B_1AA_1D_1\), в которой \(AA_1D_1\) приняли за основание. Тогда \(B_1\) – вершина. И нам нужно из \(B_1\) провести перпендикуляр к \(AA_1D_1\). Это \(B_1A_1\), то есть ребро куба
Рассматриваем искомый объем как разность объемов двух пирамид.
Vпир = S*h/3.
Для расчетов нужна площадь основания и перпендикуляр (высота) к ней
Так как это куб - то все ребра равны и перпендикулярны => ребро куба берем как высоту для пирамиды.
-----
Высота в треугольнике в данной задаче для расчетов не нужна
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
Ваш первичный балл: 0
Ваш тестовый балл: 0