Варианты ЕГЭ база (с разбором)
Содержание
Вариант ЕГЭ база 1.18
Вычислите \(\left(2\dfrac{4}{5} – 2\dfrac{3}{8}\right)⋅16\)
Найдите значение выражения \(\dfrac{1{,}4⋅ 10^{3}}{7⋅10^{-1}}\).
Ежемесячная плата за телефон составляет 250 рублей в месяц. В следующем году она увеличится на 4%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
Площадь поверхности прямоугольного параллелепипеда с рёбрами \(a\), \(b\) и \(c\) вычисляется по формуле \(S = 2(ab + bc + ac)\). Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами 3, 4 и 5.
Найдите значение выражения \((8\sqrt{7}+4)(8\sqrt{7}-4)\).
В среднем за день во время конференции расходуется 60 пакетиков чая. Конференция длится 6 дней. В пачке чая 100 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
Решите уравнение \(x^2 + 4 = 5x\). Если уравнение имеет более одного корня, укажите в ответ меньший из них.
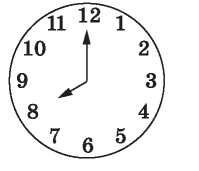
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 20:00?
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) высота горы Эверест | 1) 3520 км |
| Б) длина реки Волги | 2) 120 см |
| В) ширина окна | 3) 20 мм |
| Г) диаметр монеты | 4) 8848 м |
11 апреля на запись в первый класс независимо друг от друга пришли два будущих первоклассника. Считая, что приходы мальчика и девочки равновероятны, найдите вероятность того, что оба ребёнка оказались девочками.
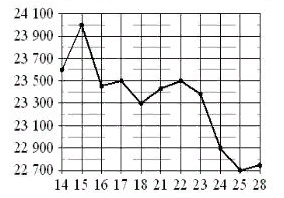
На диаграмме жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 14 по 28 ноября 2007 года. По горизонтали указываются числа месяца, по вертикали – цена олова в долларах США за тонну. Для наглядности жирные точки соединены линиями. Определите наименьшую цену олова на момент закрытия торгов в период с 14 по 21 ноября. Ответ дайте в долларах США за тонну.
Телефонная компания предоставляет на выбор три тарифных плана. Абонент предполагает, что общая длительность разговоров составит 700 минут в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна 700 минутам?
| Тарифный план | Абонентская плата (в месяц) | Плата за 1 минуту разговора |
| "Повременный" | Нет | 1,5 руб. |
| "Комбинированный" | 290 руб. за 300 мин. | 2 руб.(сверх 300 мин. в месяц) |
| "Безлимитный" | 1200 | Нет |
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
На графике изображена зависимость крутящего момента двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси – крутящий момент в Н⋅м.

Пользуясь графиком, поставьте в соответствие каждому интервалу числа оборотов в минуту характеристику крутящего момента.
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
| А) 0 - 1000 об./мин. | 1) Самый быстрый рост крутящего момента при увеличении числ оборотов |
| Б) 1500 - 2000 об./мин. | 2) При увеличении числа оборотов крутящий момент падает |
| В) 3000 - 4000 об./мин. | 3) При увеличении числа оборотов крутящий момент не меняется |
| Г) 4000 - 6000 об./мин. | 4) Крутящий момент не превышает 20 Н⋅м на всем интервале |
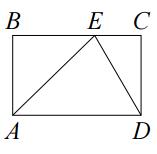
На стороне \(BC\) прямоугольника \(ABCD\), у которого \(AB = 36\) и \(AD = 113\), отмечена точка \(E\) так, что \(\angle EAB = 45°\). Найдите \(ED\).
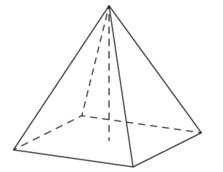
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро \(\sqrt{17}\).
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А)\((x-1)^2(x-4) < 0\) | 1) \((-\infty;1)\cup(4;+\infty)\) |
| Б) \(\dfrac{x-1}{x-4} > 0\) | 2)\((1:4)\cup(4;+\infty)\) |
| В) \((x-1)(x-4) < 0\) | 3)\((-\infty;1)\cup(1;4)\) |
| Г) \(\dfrac{(x-4)^2}{x-1} > 0\) | 4)\((1;4)\) |
В фирме N работают 60 человек, из них 50 человек знают английский язык, а 15 человек – французский. Выберите утверждения, которые следуют из привёденных данных.
В фирме N
1) если один человек знает французский язык, то он знает и английский язык.
2) хотя бы три человека знают оба языка.
3) не больше 15 человек знают два иностранных языка.
4) нет ни одного человека, знающего и английский, и французский языки.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Вычеркните в числе 23462141 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите наибольшее такое число.
В обменном пункте можно совершить одну из операций:
1) За 4 золотых монеты получить 5 серебряных и одну медную;
2) За 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?