Сборники ЕГЭ профиль
Меню курса
15 вариант Ященко ЕГЭ 2020
Часы стоили 1200 рублей. После снижения цены они стали стоить 972 рубля. На сколько процентов была снижена цена на часы?
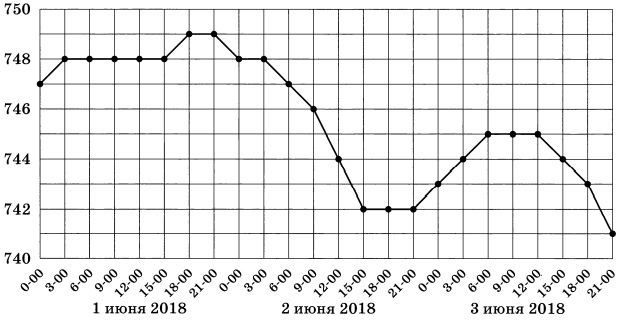
На диаграмме показано изменение атмосферного давления в Казани с 1 по 3 июня 2018 года. По горизонтали указано время, по вертикали — атмосферное давление в миллиметрах ртутного столба. Определите по рисунку наибольшее и наименьшее значения атмосферного давления (в миллиметрах ртутного столба) 3 июня 2018 года в Казани. Запишите в ответ разность этих значений.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его высоты, проведённой к прямой, содержащей сторону АВ.

По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,95. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что оба магазина доставят товар.
Найдите корень уравнения \(\sqrt{15-2x}=x\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней
В треугольнике \(ABC\) известно, что \(AC=BC\), \(AB=20\), \(\sin{A}=\dfrac{\sqrt{5}}{3}\). Найдите длину стороны \(AC\).
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2, ..., x_9\). Найдите количество точек, лежащих на промежутках возрастания функции \(f(x)\).

Площадь боковой поверхности конуса равна 30. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 2:3, считая от вершины конуса. Найдите площадь боковой поверхности отсечённого конуса.
Найдите значение выражения \(\log_{3}{32}\cdot\log_{2}{9}\)
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: \(T(t)=T_0+bt+at^2\), где \(t\) - время (в мин.), \(Т_0=1600\, К\), \(a=-5\, К/мин^2\), \(b=105\, К/мин\). Известно, что при температуре нагревательного элемента свыше \(1870 \,К\) прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
От пристани A к пристани B, расстояние между которыми равно 208 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Найдите точку максимума функции \(y=(x+7)^2\cdot e^{-1-x}\)
а) Решите уравнение \(\dfrac{4}{\sin^2{\left(\frac{7\pi}{2}-x\right)}}-\dfrac{11}{\cos{x}}+6=0\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\frac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F – середина ребра AS.
а) Постройте прямую пересечения плоскостей SAD и BCF.
б) Найдите угол между плоскостями SAD и BCF.
Решите неравенство \(9^{x+\frac{1}{9}}-4\cdot 3^{x+\frac{10}{9}}+27\geqslant0\)
Четырёхугольник ABCD вписан в окружность, причём сторона CD – диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность – в точке F, причём H – середина AE.
а) Докажите, что четырёхугольник BCFE – параллелограмм.
б) Найдите площадь четырёхугольника ABCD, если известно, что AB=5 и AH=4.
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Сколько рублей нужно вернуть банку в течение первого года кредитования?
Найдите все значения \(а\), при каждом из которых функция \(f(x)=x^2-3|x-a^2|-5x\) имеет более двух точек экстремума.
В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам некоторого отдела на общую сумму 600000 рублей (размер премии каждого сотрудника — целое число, кратное 1000). Бухгалтеру дают распределение премий, и он должен их выдать без сдачи и размена, имея 100 купюр по 1000 рублей и 100 купюр по 5000 рублей.
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, если ведущему специалисту надо выдать 40 000 рублей, а остальное поделить поровну на 70 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.