Все темы ЕГЭ
Меню курса
Геометрический смысл производной
На рисунке изображены график функции \(y=f(x) \) и касательная к этому графику, проведенная в точке с абциссой \(x_0\). Найдите значение производной функции \(f(x) \) в точке \(x_0\).
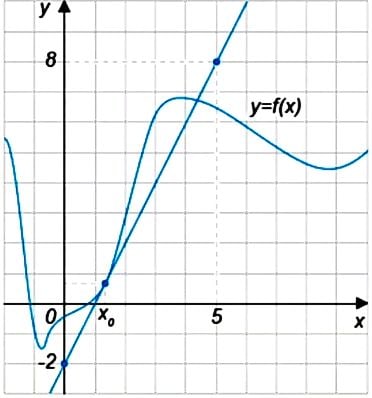
На рисунке изображён график функции \(y=f(x)\) и касательная к нему в точке с абциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).

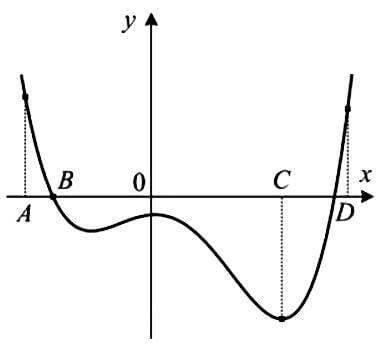
На рисунке изображён график функции \(y=f(x)\) и отмечены точки \(A{,}\, B{,}\, C\) и \(D\) на оси \(x\). Пользуясь графиком, поставьте в соответствие каждой точке (обозначено буквами) характеристику функции и ее производной (обозначено цифрами)
| Точка: | Характеристика: |
| А) A | 1) производная равна 0, функция отрицательна |
| Б) B | 2) функция положительна, производная отрицательна |
| В) C | 3) производная положительна, функция положительна |
| Г) D | 4) функция равна 0, производная отрицательна |
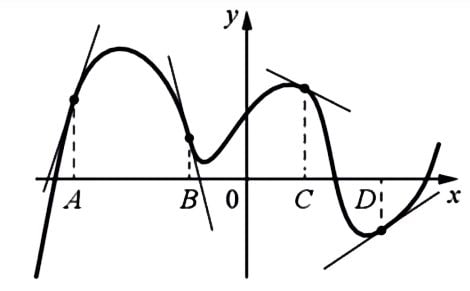
На рисунке изображены график функции и касательные, проведённые к нему в точках с абциссами \(A,\, B,\, C\) и \(D\). В правом столбце указаны значения производной функции в точках \(A,\, B,\, C\) и \(D \). Пользуясь графиком поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) \(-4\) |
| B | 2) \(3\) |
| C | 3) \(\dfrac{2}{3} \) |
| D | 4) \(-\dfrac{1}{2} \) |
На рисунке изображены график функции и касательные, проведенные к нему в точках с абциссами \(A,\, B,\, C\) и \(D\). Пользуясь графиком, поставьте в соответствие каждой точке (обозначено буквами) значение производной функции в ней (обозначено цифрами).
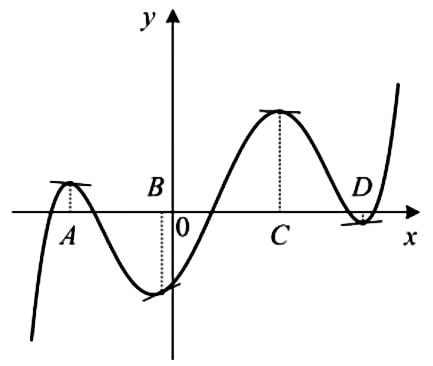
| Точка: | Производная: |
| А) A | 1) \(\dfrac{1}{2} \) |
| Б) B | 2) \(\dfrac{1}{10} \) |
| В) C | 3) \(-\dfrac{2}{25} \) |
| Г) D | 4) \(-\dfrac{1}{25} \) |
На рисунке изображён график производной функции \(f(x) \), определенной на интервале \((-6;5)\). В какой точке отрезка \([-5;-1]\) функция \(f(x)\) принимает наименьшее значение?

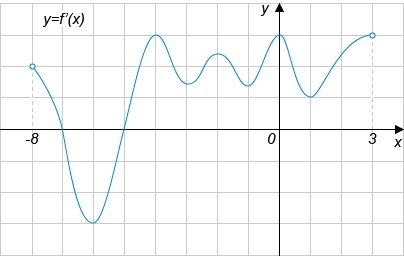
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\), определенной на интервале \((-8;3)\). В какой точке отрезка \([-3;2]\) функция \(f(x)\) принимает наибольшее значение?
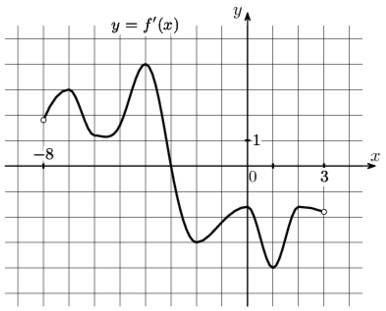
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\), определённой на интервале \((-2;9)\). В какой точке отрезка \([-1;3]\) функция \(f(x)\) принимает наибольшее значение?
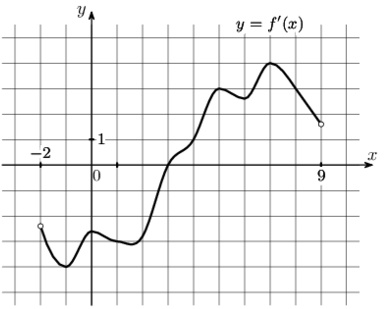
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\), определённой на интервале \((-4;8)\). Найдите точку экстремума функции \(f(x)\), принадлежащую отрезку \([-2;6]\)
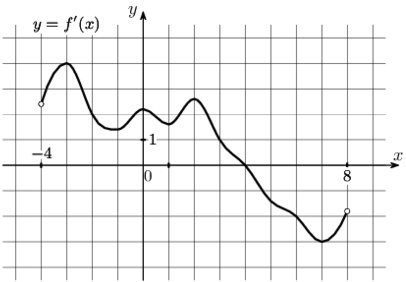
На рисунке изображён график производной функции \(f(x)\), определенной на интервале \((-9;9)\). Найдите количество точек минимума функции \(f(x)\) на отрезке \([-6;8]\)
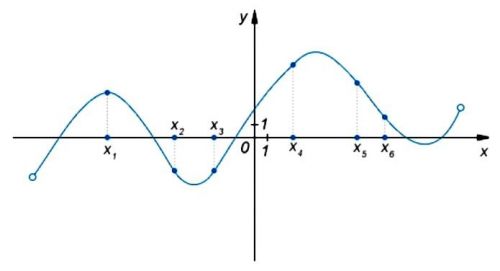
На рисунке изображен график функции и отмечены шесть точек на оси абсцисс: \(x_1, x_2, x_3,x_4, x_5, x_6\). Сколько среди этих точек таких, в которых производная функции отрицательна?
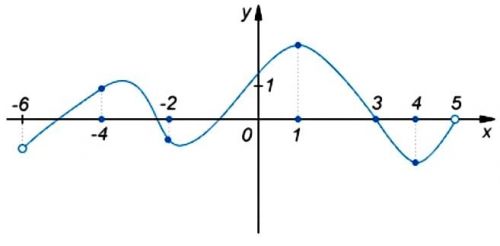
На рисунке изображен график функции, определенной на промежутке (-6;5) и отмечены пять точек на оси абсцисс: -4, -2, 1, 3, 4. В какой из этих точек значение производной наибольшее?
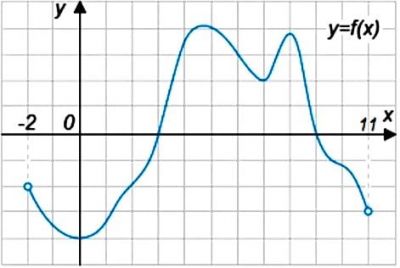
На рисунке изображен график функции \(y=f(x)\). Найдите количество целых точек интервала (-2;11), в которых производная функции \(f(x)\) положительна.
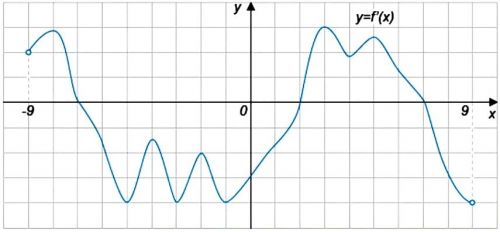
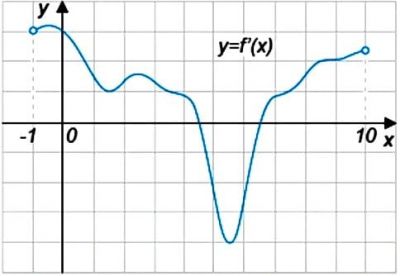
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-1;10). Найдите промежутки убывания функции \(f(x)\). В ответе укажите сумму целых точек, входящих в эти промежутки.
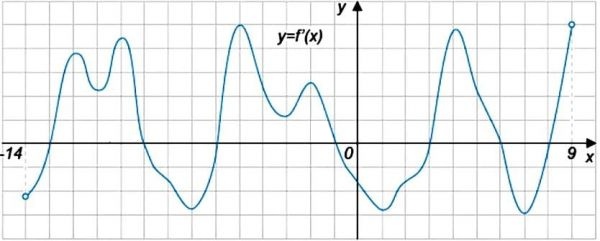
На рисунке изображен график производной функции \(f(x)\), определенной на интервале (-14;9). Найдите количество точек максимума функции \(f(x)\) на отрезке [-12;7]
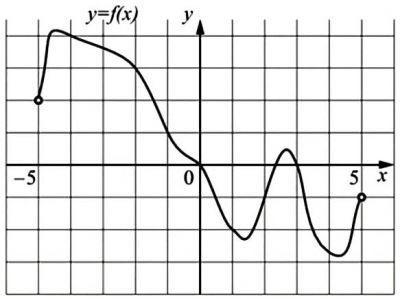
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции \(f(x)\) отрицательна.
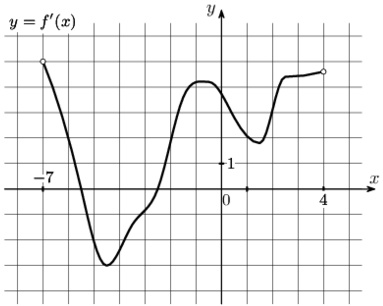
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-7;4). Найдите промежутки возрастания функции \(f(x)\). В ответ укажите сумму целых точек, входящих в эти промежутки.
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-11;3). Найдите промежутки возрастания функции \(f(x)\). В ответ укажите длину наибольшего из них.
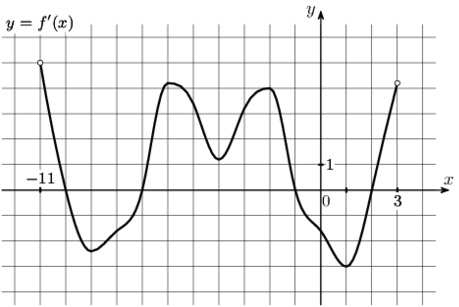
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-2;12). Найдите промежутки убывания функции \(f(x)\). В ответе укажите длину наибольшего из них.
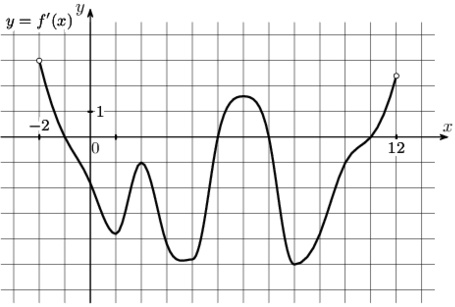
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале (-11;11). Найдите количество точек экстремума функции \(f(x)\), принадлежащих отрезку [-10;10].
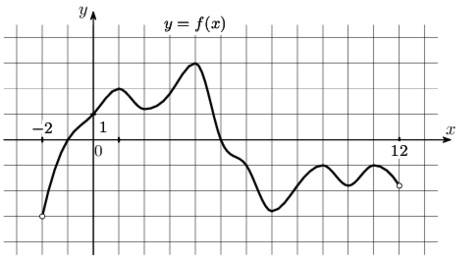
На рисунке изображен график функции y=f(x) определенной на интервале (-2;12). Найдите сумму точек экстремума функции f(x).
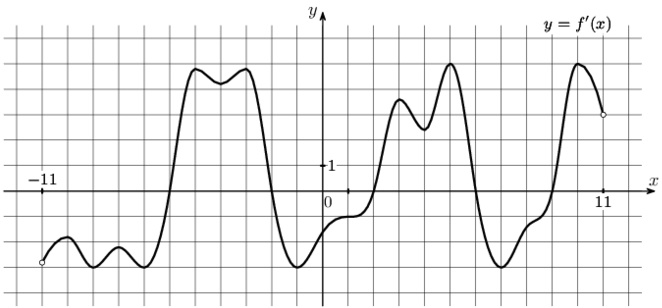
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечены восемь точек: \(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8\). Сколько из этих точек принадлежит промежуткам возрастания функции \(f(x)\)?
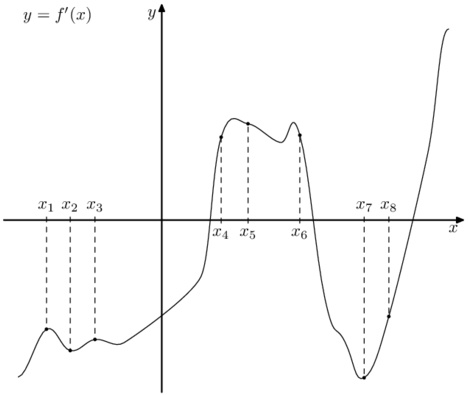
На рисунке изображен график \(y=f(x)\). На оси абсцисс отмечены восемь точек: \(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8\). В ответе укажите количество точек (из отмеченных), в которых производная функции \(f(x)\) положительна.
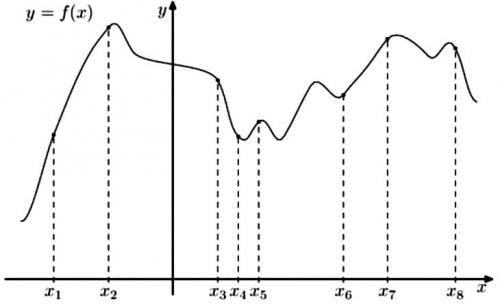
На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
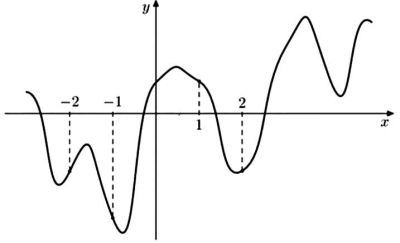
На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
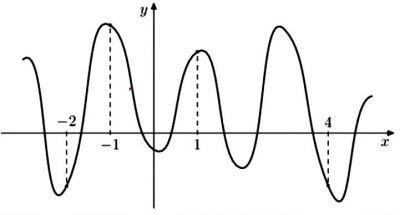
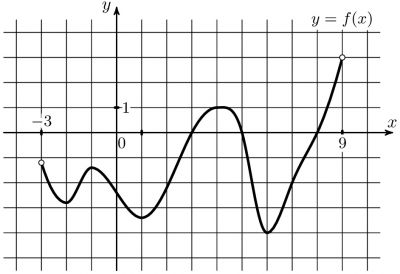
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-3;9). Определите количество точек, в которых производная функции \(f(x)\) равна 0.
На рисунке изображен график производной функции \(y=f(x)\), определенной на интервале (-8;3). Найдите количество точек, в которых касательная к графику функции \(f(x)\) параллельна прямой \(y=-20\) или совпадает с ней.