Все темы ЕГЭ
Меню курса
Многогранники
Ребро куба равно \(\sqrt{12}\). Найдите длину его диагонали.
Диагональ куба равна \(\sqrt{12}\). Найдите его объем.
Найдите объем прямоугольного параллелепипеда, ребра которого равны 3, 5, 6.
Найдите площадь поверхности прямоугольного параллелепипеда, ребра которого равны 4, 5, 6.
Если все ребра куба увеличить на 2, то площадь его поверхности увеличится на 120. Найдите ребро куба.
Гранью параллелепипеда является ромб со стороной 4 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетом 3 и гипотенузой 5, а её боковое ребро равно 10. Найдите объем призмы.
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Найдите объем призмы, основанием которой является правильный шестиугольник со стороной 4, а боковое ребро равно 5 и наклонено к плоскости основания под углом 60°.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 18. Найдите площадь боковой поверхности исходной призмы.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем исходной призмы равен 36. Найдите объем отсеченной треугольной призмы.
Стороны основания правильной четырехугольной пирамиды равны 5√2, боковые ребра равны 13. Найдите объем этой пирамиды.
Стороны основания правильной четырехугольной пирамиды равны 12, боковые ребра равны 10. Найдите площадь поверхности этой пирамиды.
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен √3.
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
От треугольной пирамиды, объем которой равен 18, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в четыре раза?
Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 24. Найдите объём треугольной пирамиды ABCA₁.
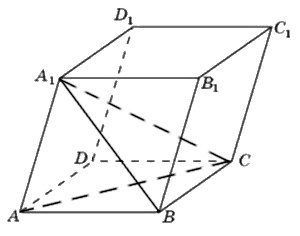
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
Объем правильной четырехугольной пирамиды SABCD (с вершиной S) равен 48. Точка E – середина ребра SB. Найдите объем треугольной пирамиды EABC.
Ребра тетраэдра равны 2. Найдите площадь сечения, проходящего через середины четырех его ребер.
Объем куба равен 24. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба.
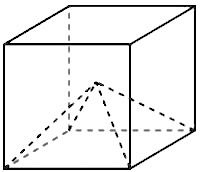
В правильной четырёхугольной пирамиде все рёбра равны 3. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
В пирамиде \(ABCD\) ребра \(DA\), \(DB\) и \(DC\) попарно перпендикулярны, а \(AB=BC=AC=6\sqrt2\).
а) Докажите, что эта пирамида правильная.
б) На ребрах \(DA\) и \(DC\) отмечены точки \(M\) и \(N\) соответственно, причем \(DM:MA=DN:NC=2:1\). Найдите площадь сечения \(MNB\).
Дана правильная четырехугольная призма \(ABCDA_1B_1C_1D_1\). На ребре \(AA_1\) отмечена точка \(K\) так, что \(AK:KA_1=1:2\). Плоскость \(\alpha\) проходит через точки \(B\), \(K\) параллельно прямой \(AC\). Эта плоскость пересекает ребро \(DD_1\) в точке \(M\).
а) Докажите, что \(MD:MD_1=2:1\).
б) Найдите площадь сечения, если \(AB=4\), \(AA_1=6\).