Досрочный ЕГЭ по математике профиль 2021

Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 21 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см

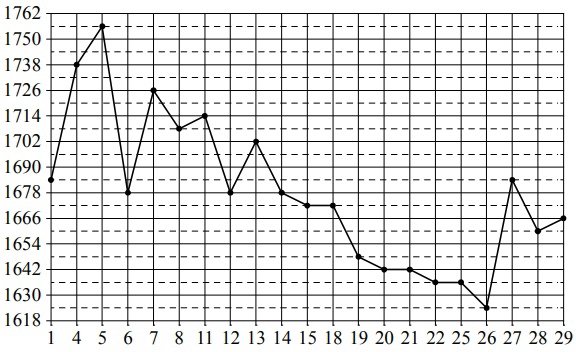
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2011 года. По горизонтали указываются числа месяца, по вертикали — цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода цена золота была равна 1678 рублям за грамм.

​

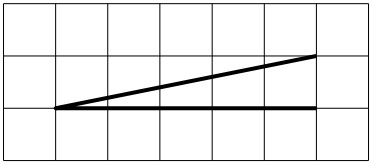
На клетчатой бумаге с размером клетки 1×1 изображён острый угол. Найдите тангенс этого угла.

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3.

Найдите корень уравнения \(\sqrt[3]{x-5}=3\)

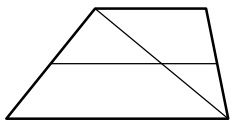
Основания трапеции равны 5 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

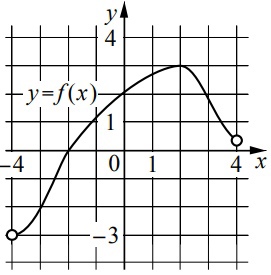
На рисунке изображён график функции \(y=f(x)\), определённой на интервале \((-4;4)  \). Найдите корень уравнения \(f'(x)=0  \)

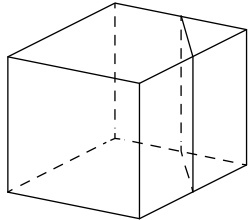
Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Найдите значение выражения \(16\log_{10}{\sqrt[4]{10}}\)

Коэффициент полезного действия (КПД) некоторого двигателя вычисляется по формуле \(η=\dfrac{T_1 - T_2}{T_1}\cdot 100\%  \), где \(T_1\) - температура нагревателя (в кельвинах), \(T_2\) -  температура холодильника (в кельвинах). При какой температуре нагревателя \(T_1\) КПД этого двигателя будет 20%, если температура холодильника \(T_2 = 336\) K? Ответ дайте в кельвинах.

Расстояние между пристанями A и B равно 165 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.

Найдите наименьшее значение функции \(y=8\mathrm{tg\,}{x}-8x-2\pi+13\) на отрезке \(\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]\)

а) Решите уравнение \(3\cdot 9^{x+1}-5\cdot 6^{x+1}+8\cdot 2^{2x}=0\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{\pi}{2};\pi\right]\)

В ответ запишите корни без пробелов через точку с запятой в порядке возрастания. Сначала на пункт А, затем на пункт Б. Например, "8;13;8"

Точка E лежит на высоте SO, а точка F - на боковом ребре SC правильной четырёхугольной пирамиды SABCD, причём SE:EO=SF:FC=2:1.
а) Докажите, что плоскость BEF пересекает ребро SD в его середине
б) Найдите площадь сечения пирамиды плоскостью, BEF если AB = 8, SO =14

Решите неравенство \(\dfrac{1}{\log_{3}{x}+4}+\dfrac{2}{\log_{3}{(3x)}} \cdot \left(\dfrac{2}{\log_{3}{x}+4}-1\right)\leqslant 0  \)

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H. Отрезок AP - диаметр окружности, описанной около треугольника ABC.
а) Докажите, что прямая HP пересекает отрезок BC в его середине.
б) Луч PH вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка MC₁, если расстояние от центра этой окружности до прямой BC равно 4, ∠BPH=120°.

В ответ введите квадрат длины этого отрезка.

15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:  
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей. 

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,25 млн рублей.

Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}2^{\ln y}=4^{|x|}\\\log_{2}(x^4y^2+2a^2)=\log_{2}{(1-ax^2y^2)+1}\end{cases}\) имеет единственное решение. 

В последовательности из 80 целых чисел каждое число (кроме первого и последнего) больше среднего арифметического соседних чисел. Первый и последний члены последовательности равны 0. 
а) Может ли второй член такой последовательности быть отрицательным?
б) Может ли второй член такой последовательности быть равным 20?
в) Найдите наименьшее значение второго члена такой последовательности. 

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.