Реальные варианты ЕГЭ и СтатГрад
Меню курса
Реальный вариант ЕГЭ 2021 по математике
Один из вариантов основной волны ЕГЭ 2021, которая прошла 7 июня. Условия задач из других вариантов вы можете посмотреть здесь: https://vk.com/topic-86125741_47816436
Решений пока нет, но вы можете прикрепить свои, нажав на синий знак вопроса на задаче после завершения теста.
В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10% от стоимости купленной мебели. Шкаф стоит 6500 рублей. Во сколько рублей обойдѐтся покупка этого шкафа вместе со сборкой?
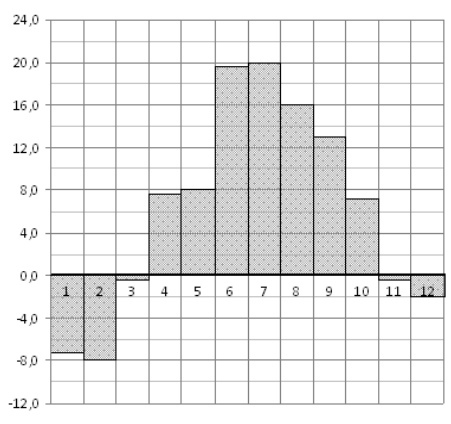
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
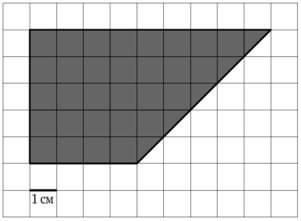
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки \(1\times 1\)
В сборнике билетов по математике всего 60 билетов, в 9 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по производной.
Найдите корень уравнения \(4^{4-x}=64\)
Один из углов прямоугольного треугольника равен 29°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах
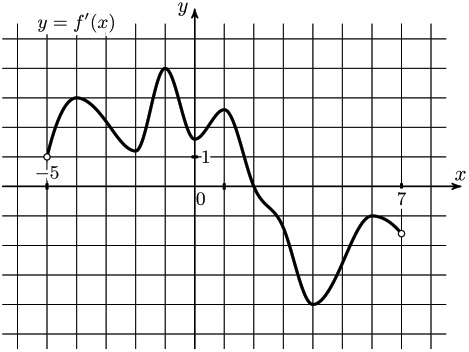
На рисунке изображен график \(y=f'(x)\) - производной функции \(f(x)\), определенной на интервале (-5;7). В какой точке отрезка [2;6] функция \(f(x)\) принимает наименьшее значение?
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.
Найдите значение выражения \(\dfrac{-14\sin{84°}}{\sin{42°}\cdot \sin{48°}}\)
В розетку электросети подключены приборы, общее сопротивление которых составляет \(R_1 =90\) Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление \(R_2\) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями \(R_1\) Ом и \(R_2\) Ом их общее сопротивление дается формулой \(R_{общ}=\dfrac{R_1 R_2}{R_1 +R_2}\) (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Решите уравнение \(\dfrac{12}{x^2+11x}=1\). Если корней несколько, в ответ запишите меньший из них.
Найдите точку максимума функции \(y=\ln{(x+10)}-5x+7\)
а) Решите уравнение \(4\sin^3{x}+3\sin{x}+2\sqrt{3}=2\sqrt{3}\cos{2x}\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\dfrac{7\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
В правильной четырехугольной пирамиде SABCD сторона основания равна 14, высота SH равна 24. Точка К – середина бокового ребра SD, а точка N – середина ребра CD. Плоскость AKB пересекает боковое ребро SC в точке P.
а) Докажите, что прямая KP пересекает отрезок SN в его середине.
б) Найдите расстояние от точки P до плоскости SAB.
Решите неравенство: \(16^{\frac{1}{x}-1}-4^{\frac{1}{x}-1}-2\geqslant 0\)
Трапеция ABCD с большим основанием AD и высотой BH вписана в окружность. Прямая BH вторично пересекает эту окружность в точке К.
а) Докажите, что прямые AC и AK перпендикулярны.
б) Прямые CK и AD пересекаются в точке N. Найдите AD, если радиус окружности равен 12, ∠BAC=30°, а площадь четырехугольника BCNH в 8 раз больше площади треугольника KNH.
В июле 2025 года планируется взять кредит в банке на сумму 700 тыс. рублей на 10 лет. Условия его возврата таковы:
- в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
- в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть полностью погашен
Найдите общую сумму выплат после полного погашения кредита.
Найдите все значения параметра \(a\), при каждом из которых уравнение \(|x^2-a^2|=|x+a|\cdot\sqrt{x^2-7ax+8a}\) имеет ровно два различных корня.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 420?
б) Может ли сумма этих чисел быть равна 419?
в) В тройке чисел первое число трѐхзначное, а третье равно 5. Сколько существует таких троек?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.