Математика 5 класс
Меню курса
Сложение натуральных чисел
Натуральные числа используются для счета предметов. Если у нас есть две группы предметов, и мы уже посчитали их количество в каждой группе, то для того, чтобы найти их общее количество не обязательно их все вместе заново пересчитывать. Для этого можно сложить количества предметов в каждой группе. Результатом этой операции будет общее количество предметов.
Сложение натуральных чисел — это арифметическое действие, с помощью которого из двух или нескольких натуральных чисел получают новое натуральное число, в котором содержится столько единиц, сколько было во всех складываемых числах вместе.
Сначала поговорим о сложении двух натуральных чисел.
Как выполняется сложение
Если к натуральному числу прибавить 1, то получится следующее натуральное число.
То есть, мы сдвигаемся по натуральному ряду на одну позицию вправо. Например, 6+1=7.

Но что делать, если к числу надо прибавить не единицу, а другое натуральное число, например 3? Можно рассуждать так: 3 — это три единицы, значит прибавить 3 это то же самое, что прибавить 1 три раза: 6+3=6+1+1+1. Чтобы узнать, чему это будет равно, будем прибавлять единицы по одной по порядку:
6+1=7
7+1=8
8+1=9
Мы к числу 6 три раза прибавили единицу и получили число 9. Значит, 6+3=9. То же самое можно увидеть, сдвинувшись по числовому ряду от числа 6 три раза на 1 место вправо.
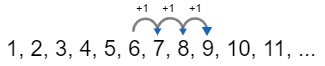
Но вместо того, чтобы три раза сдвигаться вправо на единицу, можно один раз сдвинуться вправо на 3.
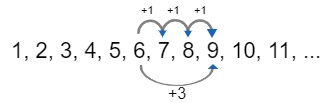
Таким образом, чтобы прибавить к натуральному числу \(a\) натуральное число \(b\), надо от \(a\) сдвинуться по числовому ряду на \(b\) позиций вправо.
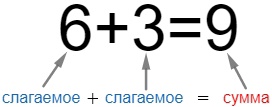
Числа, которые складываются, называются слагаемыми. А результат их сложения называется суммой.
Сложение по координатному лучу
Вместо натурального ряда для сложения можно использовать координатный луч. Действуем похожим образом: чтобы прибавить к числу \(a\) число \(b\), надо из точки с координатой \(a\) сдвинуться на \(b\) единичных отрезков вправо. Это то же самое, что по натуральному ряду сдвинуться вправо на \(b\) позиций.
Для нашего примера 6+3=9 это будет выглядеть так:
