7 вариант ЕГЭ Ященко с решением

Стоимость проездного билета на месяц составляет 1450 рублей, а стоимость билета на одну поездку - 46 рублей. Ира купила проездной и сделала за месяц 48 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?

В ходе химической реакции масса исходного вещества (реагента), которое ещё не вступило в реакцию, постепенно уменьшается. На графике показана зависимость массы реагента от времени. На горизонтальной оси отмечено время, прошедшее с начала реакции, в минутах, на вертикальной оси - масса реагента, который ещё не вступил в реакцию, в граммах. Определите по графику, сколько граммов реагента останется через 1 минуту после начала реакции.

​

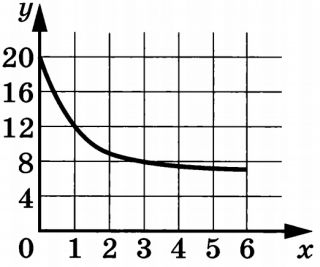
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

​

Научная конференция проводится в 4 дня. Всего запланировано 50 докладов: первые два дня по 13 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Найдите корень уравнения \(\bigg(\dfrac1{4}\bigg)^{x-2{,}5}=\dfrac1{8}\)

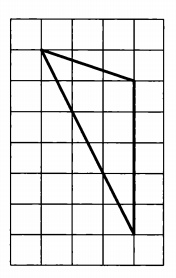
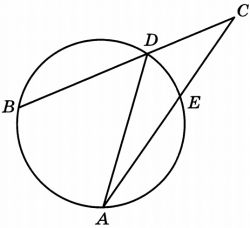
Градусная мера дуги AB окружности, не содержащей точку D, равна 106°. Градусная мера дуги DE окружности, не содержащей точку A, равна 48°. Найдите угол ACB. Ответ дайте в градусах.

​

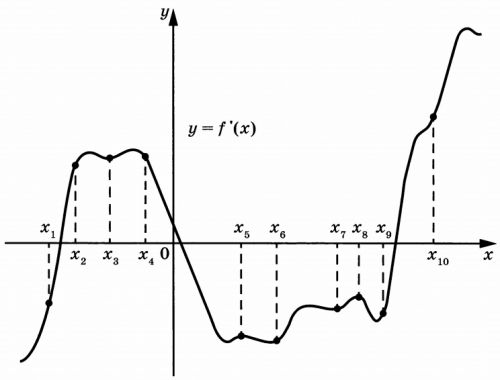
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\). На оси абсцисс отмечены 10 точек: \(x_1\), \(x_2\), \(x_3\), \(x_4\), \(x_5\), \(x_6\), \(x_7\), \(x_8\), \(x_9\), \(x_{10}\). Сколько из этих точек лежит на промежутках убывания функции \(f(x)\)?

​

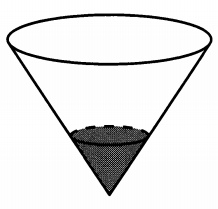
В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

​

Найдите значение выражения \(4\cos4\alpha\), если \(\sin2\alpha=-0{,}4\).

Независимое агентство намерено ввести рейтинг \(R\) новостных изданий на основе показателей информативности \(In\), оперативности \(Op\) и объективности \(Tr\) публикаций. Каждый отдельный показатель - целое число от -1 до 1. Составители рейтинга считают, что информативность публикаций ценится вчетверо, а объективность - вдвое дороже, чем оперативность, то есть \(R=\dfrac{4In+Op+2Tr}{A}\). Найдите, каким должно быть число \(A\), чтобы издание, у которого все показатели максимальны, получило рейтинг 1.

Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 63 км/ч, а вторую половину пути - со скоростью, большей скорости первого на 22 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

Найдите точку минимума функции \(y=11x-\ln(x+4)^{11}-3\).

а) Решите уравнение \(\sin\bigg(2x+\dfrac{2\pi}{3}\bigg)\cos\bigg(4x+\dfrac{\pi}{3}\bigg)-\cos2x=\dfrac{\sin^2x}{\cos\left(-\dfrac{\pi}{3}\right)}\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\bigg[-2\pi;\dfrac{3\pi}{2}\bigg]\).

Выберите все верные ответы на пункты а) и б)

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB равна 2√3, а боковое ребро AA₁ равно 3. На рёбрах A₁D₁ и DD₁ отмечены соответственно точки K и M так, что A₁K=KD₁, а DM:MD₁=2:1.
а) Докажите, что прямые MK и BK перпендикулярны.
б) Найдите угол между плоскостями BMK и BCC₁. Ответ дайте в градусах.

Решите неравенство \(\dfrac{6\cdot5^x-11}{25^{x+0,5}-6\cdot5^x+1}\geqslant0{,}25\)

На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.
а) Докажите, что LC – высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC=4.

Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоит 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30%. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?

Найдите, при каких неотрицательных значениях \(a\) функция \(f(x)=3ax^4-8x^3+3x^2-7\) на отрезке \([-1;1]\) имеет ровно одну точку минимума.

Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1).
а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 9 нулями?
б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 23 нулями?
в) Сколько существует натуральных чисел n, меньших 100, для каждого из которых десятичная запись числа n!⋅(100-n)! оканчивается ровно 23 нулями?

Введите ответ в форме строки "да;нет;1234", где ответы на пункты разделены ";", и первый ответ с маленькой буквы.