36 вариантов ЕГЭ 2021
Меню курса
27 вариант ЕГЭ Ященко с решением
На бензоколонке один литр бензина стоит 33 рубля 20 копеек. Водитель залил в бак 25 литров бензина и взял бутылку воды за 25 рублей. Сколько рублей сдачи он получит с 1000 рублей?
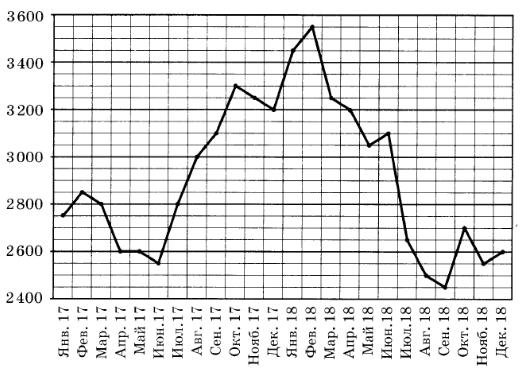
На рисунке показана средняя цена цинка во все месяцы 2017 и 2018 годов. По горизонтали указаны месяцы, по вертикали - цена тонны цинка в долларах США. Для наглядности точки соединены отрезками. Определите, на сколько долларов стала ниже цена тонны цинка в сентябре 2018 года по сравнению с сентябрём 2017 года.
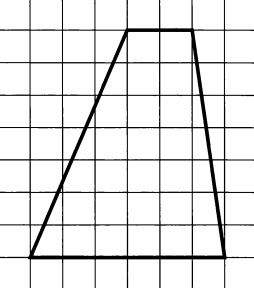
На клетчатой бумаге с размером клетки \(1\times 1\) изображена трапеция. Найдите длину средней линии этой трапеции.
В группе туристов 20 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист В., входящий в состав группы, полетит первым рейсом вертолёта.
Найдите корень уравнения \(\sqrt{7x-31}=2\)
Площадь параллелограмма ABCD равна 28. Точка Е - середина стороны AD. Найдите площадь трапеции BCDE.

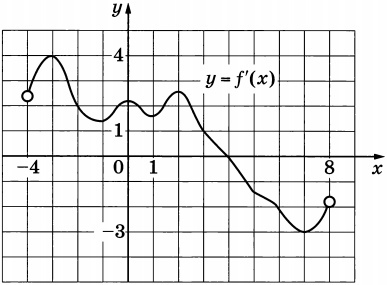
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\), определённой на интервале (-4;8). Найдите точку экстремума функции \(f(x)\), принадлежащую отрезку [1;6].
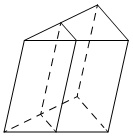
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 36. Найдите площадь боковой поверхности исходной призмы.
Найдите значение выражения \((\sqrt{96}-\sqrt{24})\cdot \sqrt{6}\)
К источнику с ЭДС \(ε=180\) В и внутренним сопротивлением \(r=1\) Ом хотят подключить нагрузку с сопротивлением \(R\) (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле \(U=\dfrac{εR}{R+r}.\) При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В? Ответ дайте в омах.
Заказ на изготовление 209 деталей первый рабочий выполняет на 8 часов быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 8 деталей больше?
Найдите наименьшее значение функции \(y=9x-\ln(x+5)^9\) на отрезке [-4,5;0]
а) Решите уравнение \((2\cos^2{x}+3\sin{x}-3)\cdot \log_{2}{(\sqrt{2}\cos{x})}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-5\pi;-3\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π | 18. -29π/6 | 19. -19π/4 | 20. -14π/3 |
| 21. -9π/2 | 22. -13π/3 | 23. -17π/4 | 24. -25π/6 |
| 25. -4π | 26. -23π/6 | 27. -15π/4 | 28. -11π/3 |
| 29. -7π/2 | 30. -10π/3 | 31. -13π/4 | 32. -19π/6 |
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания – точка C₁, причём CC₁ – образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=45°, AB=3√2, CC₁=6.
а) Докажите, что угол между прямыми AC₁ и BC равен 60°.
б) Найдите расстояние от точки B до прямой AC₁.
Решите неравенство: \(\log_{5}{\left(\dfrac{3}{x}+2\right)}-\log_{5}{(x+2)}\leqslant \log_{5}{\left(\dfrac{x+1}{x^2}\right)}\)
Окружность с центром O₁ касается оснований ВС и АD, а также боковой стороны АВ трапеции ABCD. Окружность с центром O₂ касается сторон ВС, СD и АD. Известно, что АВ=9, ВС=8, СD=4, АD=15.
а) Докажите, что прямая O₁O₂ параллельна основаниям трапеции ABCD.
б) Найдите O₁O₂
15-го марта планируется взять кредит в банке на 26 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1924 тысячи рублей? Ответ дайте в тысячах рублей.
Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\begin{cases}x^4+y^2=a^2\\x^2+y=|a+1|\end{cases}\) имеет ровно четыре решения.
На доске написано 12 различных натуральных чисел. Среднее арифметическое семи наименьших из них равно 8, а среднее арифметическое семи наибольших равно 16.
а) Может ли наибольшее из этих двенадцати чисел равняться 18?
б) Может ли среднее арифметическое всех двенадцати чисел равняться 11?
в) Найдите наименьшее значение среднего арифметического всех двенадцати чисел
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.