36 вариантов ЕГЭ 2021
Меню курса
28 вариант ЕГЭ Ященко с решением
Стоимость полугодовой подписки на журнал составляет 720 рублей, а стоимость одного номера журнала - 36 рублей. За полгода Аня купила 25 номеров журнала. На сколько рублей меньше она бы потратила, если бы подписалась на журнал?
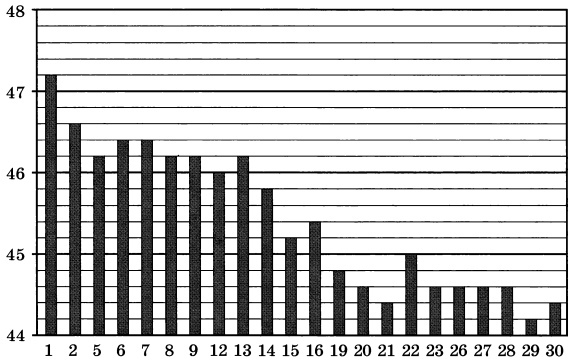
На диаграмме показан курс южноафриканского рэнда, установленный Центробанком РФ на все рабочие дни марта 2019 года. По горизонтали указаны числа месяца, по вертикали - цена 10 южноафриканских рэндов в рублях. Определите наименьшую цену в рублях 10 южноафриканских рэндов в период с 13 по 23 марта 2019 года.
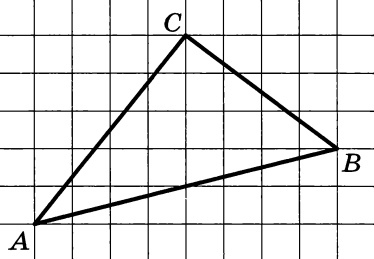
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
На конференцию приехали учёные из трёх стран: 7 из Сербии, 3 из России и 2 из Дании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад учёного из России.
Найдите корень уравнения \(\sqrt[3]{x+6}=4\)
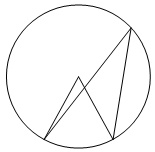
Найдите центральный угол, если он на 28° больше острого вписанного угла, опирающегося на ту же дугу. Ответ дайте в градусах.
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).

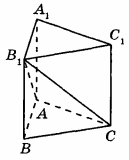
Дана правильная треугольная призма ABCA₁B₁C₁ площадь основания которой равна 8, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки A, C, A₁, B₁, C₁
Найдите значение выражения \(\left(2^{16}\right)^5:2^{74}\)
Мотоциклист, движущийся по городу со скоростью \(v_0=60\,км/ч\), выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением \(a=18\, км/ч^2.\) Расстояние (в км) от мотоциклиста до города вычисляется по формуле \(S=v_0 t+\dfrac{at^2}{2}\) где \(t\) - время в часах, прошедшее после выезда из города. Определите время, прошедшее после выезда мотоциклиста из города, если известно, что за это время он удалился от города на 21 км. Ответ дайте в минутах.
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 285 литров она заполняет на 4 минуты дольше, чем вторая труба?
Найдите наименьшее значение функции \(y=12x-\ln(12x)+4\) на отрезке \(\left[\dfrac{1}{24};\dfrac{5}{24}\right]\)
а) Решите уравнение: \((2\sin^2x-\cos x-1)\log_{3}{(-0{,}2\sin x)}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку: \([5\pi;7\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π | 18. 31π/6 | 19. 21π/4 | 20. 16π/3 |
| 21. 11π/2 | 22. 17π/3 | 23. 23π/4 | 24. 35π/6 |
| 25. 6π | 26. 37π/6 | 27. 25π/4 | 28. 19π/3 |
| 29. 13π/2 | 30. 20π/3 | 31. 27π/4 | 32. 41π/6 |
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания - точка C₁, причём CC₁ - образующая цилиндра, а AC - диаметр основания. Известно, что ∠ACB=30°, AB=√2, CC₁=4
а) Докажите, что угол между прямыми AC₁ и BC равен 60°
б) Найдите площадь боковой поверхности цилиндра.
Решите неравенство: \(15^x-9\cdot 5^x-3^x+9\leqslant 0\)
Окружность с центром O₁ касается оснований ВС и АD, а также боковой стороны АВ трапеции ABCD. Окружность с центром O₂ касается сторон ВС, СD и АD. Известно, что АВ=15, ВС=32, СD=14, АD=11.
а) Докажите, что прямая O₁O₂ параллельна основаниям трапеции ABCD.
б) Найдите O₁O₂
15 июля планируется взять кредит в банке на сумму 1400 тысяч рублей на 31 месяц. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
- 15-го числа 30-го месяца долг составит 500 тысяч рублей;
- к 15-му числу 31-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1989 тысяч рублей.
Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\begin{cases}x^4+y^2=a^2-1\\x^2-y=|a-1|\end{cases}\) имеет ровно четыре решения.
На доске написано 11 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 8, а среднее арифметическое семи наибольших равно 14.
а) Может ли наибольшее из этих одиннадцати чисел равняться 16?
б) Может ли среднее арифметическое всех одиннадцати чисел равняться 10?
в) Найдите наименьшее значение среднего арифметического всех одиннадцати чисел.
Введите ответ в форме строки "да;да;23:34", где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а ответ на пункт в) в виде не сократимого отношения, записанного через ":".