36 вариантов ЕГЭ 2021
Меню курса
23 вариант ЕГЭ Ященко с решением
Таксист за месяц проехал 11 000 км. Цена бензина 35 рублей за литр. Средний расход бензина на 100 км составляет 7 литров. Сколько рублей потратил таксист на бензин за этот месяц?
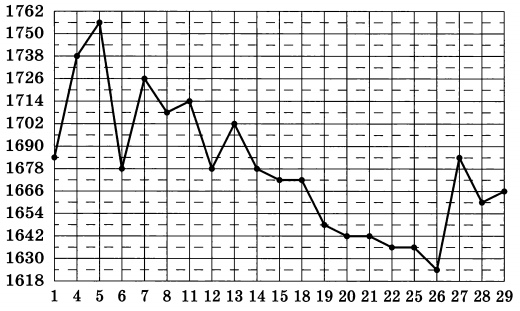
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2011 года. По горизонтали указываются числа месяца, по вертикали – цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену золота в период с 1 по 11 октября (в рублях за грамм).
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите длину его большей высоты.

В группе туристов 12 человек. С помощью жребия они выбирают трёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Найдите корень уравнения \(\sqrt{3x+49}=10\)
Найдите угол АСО, если его сторона СА касается окружности с центром О, отрезок СО пересекает окружность в точке В (см. рис.), а дуга АВ окружности, заключённая внутри этого угла, равна 17°. Ответ дайте в градусах.

На рисунке изображён график функции \(y=f(x)\), определённой на интервале \((-7; 8)\). \(F(x)\) – одна из первообразных функции \(y=f(x)\). Найдите количество точек, в которых касательная к графику функции \(F(x)\) параллельна прямой \(y=-x+2\) или совпадает с ней.

Найдите объём многогранника, вершинами которого являются вершины \(A, B, C, D, B_1\) прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\), у которого \(AB=9\), \(BC=3\), \(BB_1=8\)

Найдите значение выражения \(\dfrac{81^{2{,}6}}{9^{3{,}7}}\)
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём меняется по закону \(H(t)=at^2+bt+H_0\),где \(H\) – высота столба воды в метрах, \(H_0=8\,м\) – начальный уровень воды, \(a=\dfrac{1}{72}\,м/мин^2\) и \(b=-\dfrac{2}{3}\,м/мин\) – постоянные, \(t\) – время в минутах, прошедшее с момента открытия крана. Сколько минут вода будет вытекать из бака?
Два велосипедиста одновременно отправились в 140-километровый пробег. Первый ехал со скоростью на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=\ln(8x)-8x+7\) на отрезке \(\left[\dfrac1{16};\dfrac5{16}\right]\)
а) Решите уравнение \(\left((0{,}04)^{\sin{x}}\right)^{\cos{x}}=5^{-\sqrt{3}\sin{x}}\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[\dfrac{5\pi}{2};4\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
Дан куб ABCDA₁B₁C₁D₁
а) Постройте сечение куба плоскостью, проходящей через точки B, A₁ и D₁
б) Найдите угол между плоскостями BA₁C₁ и BA₁D₁
Решите неравенство: \(\log_{2}{(x^2-2)}-\log_{2}{x}\leqslant\log_{2}{\left(x-\dfrac{2}{x^2}\right)}\)
Окружность с центром в точке O пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках E и F так, что AE=19, EF=12, FB=3.
15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
– 15-го числа 15-го месяца долг составит 100 тысяч рублей;
– к 15-му числу 16-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}(a+1)(x^2+y^2)+(a-1)x+(a+1)y+2=0\\xy-1=x-y\end{cases}\) имеет ровно четыре различных решения.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 12 раз больше, либо в 12 раз меньше предыдущего. Сумма всех членов последовательности равна 8750.
а) Может ли последовательность состоять из двух членов?
б) Может ли последовательность состоять из трёх членов?
в) Какое наибольшее количество членов может быть в последовательности?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.