36 вариантов ЕГЭ 2021
Меню курса
25 вариант ЕГЭ Ященко с решением
Часы стоили 1200 рублей. После снижения цены они стали стоить 972 рубля. На сколько процентов была снижена цена на часы?
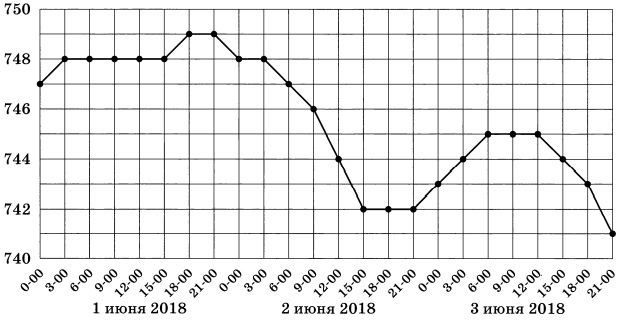
На диаграмме показано изменение атмосферного давления в Казани с 1 по 3 июня 2018 года. По горизонтали указано время, по вертикали — атмосферное давление в миллиметрах ртутного столба. Определите по рисунку наибольшее и наименьшее значения атмосферного давления (в миллиметрах ртутного столба) 3 июня 2018 года в Казани. Запишите в ответ разность этих значений.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его высоты, проведённой к прямой, содержащей сторону АВ.

По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,95. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что оба магазина доставят товар.
Найдите корень уравнения \(\sqrt{15-2x}=x\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней
В треугольнике \(ABC\) известно, что \(AC=BC\), \(AB=20\), \(\sin{A}=\dfrac{\sqrt{5}}{3}\). Найдите длину стороны \(AC\).
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2, ..., x_9\). Найдите количество точек, лежащих на промежутках возрастания функции \(f(x)\).

Площадь боковой поверхности конуса равна 30. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 2:3, считая от вершины конуса. Найдите площадь боковой поверхности отсечённого конуса.
Найдите значение выражения \(\log_{3}{32}\cdot\log_{2}{9}\)
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: \(T(t)=T_0+bt+at^2\), где \(t\) - время (в мин.), \(Т_0=1600\, К\), \(a=-5\, К/мин^2\), \(b=105\, К/мин\). Известно, что при температуре нагревательного элемента свыше \(1870 \,К\) прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
От пристани A к пристани B, расстояние между которыми равно 208 км, отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью на 3 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Найдите точку максимума функции \(y=(x+7)^2\cdot e^{-1-x}\)
а) Решите уравнение \(\dfrac{4}{\sin^2{\left(\frac{7\pi}{2}-x\right)}}-\dfrac{11}{\cos{x}}+6=0\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\frac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F – середина ребра AS.
а) Постройте прямую пересечения плоскостей SAD и BCF.
б) Найдите угол между плоскостями SAD и BCF.
Решите неравенство \(9^{x+\frac{1}{9}}-4\cdot 3^{x+\frac{10}{9}}+27\geqslant0\)
Четырёхугольник ABCD вписан в окружность, причём сторона CD – диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность – в точке F, причём H – середина AE.
а) Докажите, что четырёхугольник BCFE – параллелограмм.
б) Найдите площадь четырёхугольника ABCD, если известно, что AB=5 и AH=4.
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Сколько рублей нужно вернуть банку в течение первого года кредитования?
Найдите все значения \(а\), при каждом из которых функция \(f(x)=x^2-3|x-a^2|-5x\) имеет более двух точек экстремума.
В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам некоторого отдела на общую сумму 600000 рублей (размер премии каждого сотрудника — целое число, кратное 1000). Бухгалтеру дают распределение премий, и он должен их выдать без сдачи и размена, имея 100 купюр по 1000 рублей и 100 купюр по 5000 рублей.
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, если ведущему специалисту надо выдать 40 000 рублей, а остальное поделить поровну на 70 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.