36 вариантов ЕГЭ 2021
Меню курса
24 вариант ЕГЭ Ященко с решением
Люда отправила SMS-сообщения с новогодними поздравлениями своим 18 друзьям. Стоимость одного SMS-сообщения 1 рубль 10 копеек. Перед отправкой сообщений на счёте у Люды было 44 рубля. Сколько рублей останется на счёте после отправки всех сообщений?
На диаграмме показана средняя цена нефти марки WTI во все месяцы 2017 и 2018 годов. По горизонтали указаны месяцы, по вертикали — цена барреля нефти в долларах США. Определите, сколько месяцев во втором полугодии 2017 года цена барреля нефти была выше 50 долларов.

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 3 прыгуна из Голландии и 6 прыгунов из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Аргентины.
Найдите корень уравнения \(4^{x-7}=\dfrac{1}{64}\)
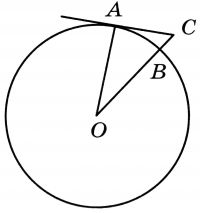
Угол ACO равен 62°. Его сторона CA касается окружности с центром в точке O. Отрезок CO пересекает окружность в точке B (см. рис.). Найдите градусную меру дуги AB окружности, заключённой внутри этого угла. Ответ дайте в градусах.
На рисунке изображён график y=f'(x) - производной функции f(x), определённой на интервале (-19;3). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-17;-4].

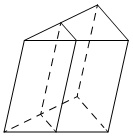
Через среднюю линию основания треугольной призмы, объём которой равен 52, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
Найдите значение выражения \(4^{\frac15}\cdot 16^{\frac9{10}}\)
Сила тока \(I\) (в А) в электросети вычисляется по закону Ома: \(I=\dfrac{U}{R}\), где \(U\) - напряжение электросети (в В), \(R\) - сопротивление подключаемого электроприбора (в Ом). Электросеть прекращает работать, если сила тока превышает 5 А. Определите, какое наименьшее сопротивление может быть у электроприбора, подключаемого к электросети с напряжением 220 В, чтобы электросеть продолжала работать. Ответ дайте в омах.
Расстояние между городами A и B равно 500 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=\ln(x+9)^5-5x\) на отрезке [-8,5;0]
а) Решите уравнение \(\left((0{,}25)^{\sin{x}}\right)^{\cos{x}}=2^{-\sqrt{2}\sin{x}}\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[2\pi;\dfrac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
Дан куб ABCDA₁B₁C₁D₁.
а) Постройте сечение куба плоскостью, проходящей через середины ребер AB, B₁C₁, AD.
б) Найдите угол между плоскостью A₁BD и плоскостью, проходящей через середины рёбер AB, B₁C₁, AD.
Решите неравенство \(\log_{5}{\left(2-\dfrac{2}{x}\right)}-\log_{5}{(x+3)}\geqslant\log_{5}{\left(\dfrac{x+3}{x^2}\right)}\)
Окружность с центром в точке O пересекает каждую из сторон трапеции ABCD в двух точках. Четыре получившиеся хорды окружности равны.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK=13, KL=6, LB=1.
15 мая планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 16-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 17-го месяца кредит должен быть полностью погашен.
Сколько рублей планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1472 тысячи рублей?
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}a(x^2+y^2)-ax+(a-3)y+1=0\\xy-1=y-x\end{cases}\) имеет ровно четыре различных решения.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 14 раз больше, либо в 14 раз меньше предыдущего. Сумма всех членов последовательности равна 7424.
а) Может ли последовательность состоять из двух членов?
б) Может ли последовательность состоять из трёх членов?
в) Какое наибольшее количество членов может быть в последовательности?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.