9 вариант ЕГЭ Ященко с решением

Для покраски 1 кв. м потолка в среднем требуется 120 г краски. Краска продаётся в банках по 1,5 кг. Егор решил купить краску с запасом в 10% к среднему расходу. Какое наименьшее количество банок краски нужно купить для покраски потолка площадью 42 кв. м?

Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На горизонтальной оси откладывается скорость в километрах в час, на вертикальной оси – подъёмная сила в тоннах силы. Определите по графику, на сколько километров в час увеличилась скорость полёта при увеличении подъёмной силы с 1 тонны до 4 тонн.

​

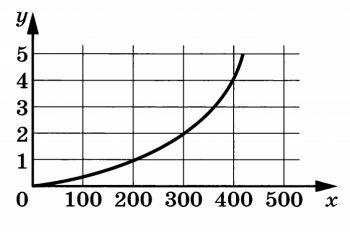
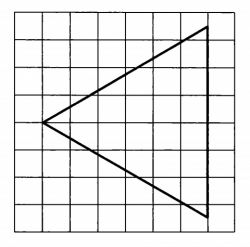
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности.

В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зеленых, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зеленых, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранная чашка и блюдце будут одинакового цвета.

Найдите корень уравнения \((2x-11)^2 = (2x-1)^2\)

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 15 и 17.

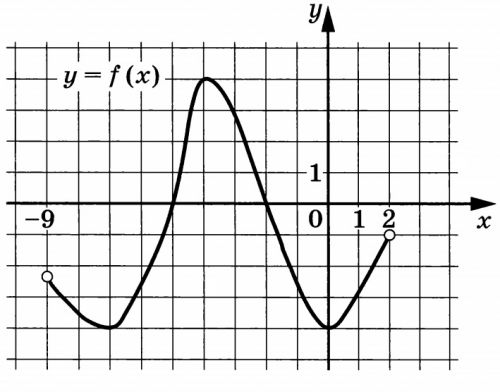
На рисунке изображён график функции \(y = f(x)\), определённой на интервале \((-9; 2)\). Определите количество целых точек, в которых производная функции отрицательна.

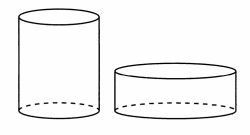
Дано два цилиндра. Объём первого цилиндра равен 5. У второго цилиндра высота в 2,5 раза меньше, а радиус основания в 3 раз больше, чем у первого. Найдите объём второго цилиндра.

​

Найдите значение выражения \(\dfrac{8^{2{,}8} \cdot 16^{2{,}4}}{32^{3{,}2}}\).

Водолазный колокол, содержащий \(\nu=5\) моль воздуха при объём \(V_1=26\,л\) , медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма \(V_2\) (в л). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log_2{\dfrac{V_1}{V_2}}\), где \(\alpha=8{,}5\, \dfrac{Дж}{моль\cdot К}\) – постоянная, \(T=300\, К\) – температура воздуха. Найдите, какой объём \(V_2\) будет занимать воздух в колоколе, если при сжатии воздуха была совершена работа в \(25500\, Дж\). Ответ дайте в литрах.

Смешали 2 кг воды с 3 кг 32-процентного раствора и некоторым количеством 42-процентного раствора одного и того же вещества. Сколько килограммов 42-процентного раствора использовали, если в результате получили 32-процентный раствор вещества?

Найдите наименьшее значение функции \(y=x\sqrt{x}-6x+11\) на отрезке \([0;30]\)

а) Решите уравнение \(\cos{3x}\sin{3x} = \cos{\dfrac{\pi}{3}}\cos{\left(12x + \dfrac{3\pi}{2}\right)}\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{3\pi}{4}; -\dfrac{\pi}{4}\right]\).

В правильной восьмиугольной призме \(ABCDEFGHA_1B_1C_1D_1E_1F_1G_1H_1\) сторона основания \(AB\) равна \(3\sqrt{2}\), а боковое ребро \(AA_1\) равно \(6\). На ребре \(CC_1\) отмечена точка \(M\) так, что \(CM : MC_1 = 1 : 2\). Плоскость \(\alpha\) параллельна прямой \(H_1E_1\) и проходит через точки \(M\) и \(A\).

а) Докажите, что сечение призмы \(ABCDEFGHA_1B_1C_1D_1E_1F_1G_1H_1\) плоскостью \(\alpha\) – равнобедренная трапеция.

б) Найдите объём пирамиды, вершиной которой является точка \(F_1\), а основанием – сечение призмы \(ABCDEFGHA_1B_1C_1D_1E_1F_1G_1H_1\) плоскостью \(\alpha\).

Решите неравенство \(9 \cdot 2^{\log_{3}{(5-x)}} + 2^{1+ \log_{3}{x}} – 2^{\log_{3}{(5x – x^2)}} \leqslant 18\)

Отрезок, соединяющий середины M и N оснований соответственно BC и AD трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность.
а) Докажите, что трапеция ABCD равнобедренная.
б) Известно, что радиус этих окружностей равен 4, а меньшее основание BC исходной трапеции равно 14. Найдите радиус окружности, касающейся боковой стороны AB, основания AN трапеции ABMN и вписанной в неё окружности.

Цена ценной бумаги на конец года вычисляется по формуле \(S = 1{,}1S_0 + 2000\), где \(S_0\) – цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12%. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тысяч рублей, которые он может положить на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.

Найдите все значения параметра \(a\), при которых система уравнений \(\begin{cases} \log_7(36 - y^2)=\log_7(36 - a^2x^2)\\x^2+y^2=2x+6y\end{cases}\) имеет ровно два различных решения.

Для набора 30 различных натуральных чисел выполнено, что сумма любых трёх чисел из этого набора меньше суммы любых четырёх числе из этого набора.
а) Может ли одним из этих чисел быть число 999?
б) Может ли одним из этих чисел быть число 66?
в) Какое наименьшее значение может принимать сумма чисел этого набора?

Введите ответ в форме строки "да;нет;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.