36 вариантов ЕГЭ 2023
Меню курса
26 вариант ЕГЭ Ященко 2023
Решение 26 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 127°. Найдите угол BCD. Ответ дайте в градусах.

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что AB=9, BC=8, AA₁=6. Найдите объём многогранника, вершинами которого являются точки A, B, C, B₁.

В магазине в одной коробке лежат вперемешку ручки с черными, синими и красными чернилами, одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется черной, равна 0,36, а того, что она окажется красной, равна 0,26. Найдите вероятность того, что ручка окажется синей.
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,97?
Найдите корень уравнения \(\sqrt{-x}=x+6\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Найдите значение выражения \(\cos\alpha\), если \(\mathrm{tg\,} \alpha=\dfrac{\sqrt{91}}{3}\) и \(\alpha\in\bigg(\pi;\dfrac{3\pi}{2}\bigg)\).
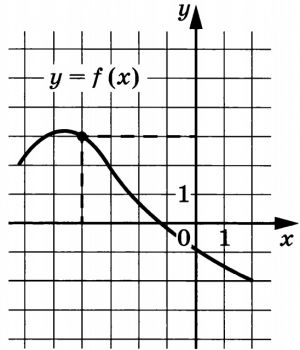
На рисунке изображён график функции \(y=f(x)\). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой \(-4\). Найдите значение производной функции в точке \(x_0=-4\).
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с фокусным расстоянием \(f = 60 \,см\). Расстояние \(d_1\) от линзы до лампочки может изменяться в пределах от 95 см до 115 см а расстояние \(d_2\) от линзы до экрана - в пределах от 140 см до 160 см. Изображение на экране будет чётким, если выполнено соотношение \(\dfrac1{d_1}+\dfrac1{d_2}=\dfrac1{f}\). На каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким? Ответ дайте в сантиметрах.
Первый и второй насосы наполняют бассейн за 35 минут, второй и третий - за 40 минут, а первый и третий - за 56 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
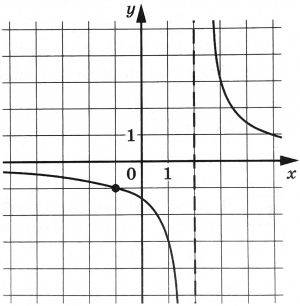
На рисунке изображён график функции \(f(x)=\dfrac{k}{x+a}\). Найдите значение \(x\), при котором \(f(x)=-0{,}2\).
Найдите наибольшее значение функции \(y=(x-6)e^{7-x}\) на отрезке \([2;15]\).
а) Решите уравнение \(\sin^2\bigg(\dfrac{x}{4}+\dfrac{\pi}{4}\bigg)\sin^2\bigg(\dfrac{x}{4}-\dfrac{\pi}{4}\bigg)=0,375\sin^2\bigg(-\dfrac{\pi}{4}\bigg)\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-3\pi;\pi]\).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -8π/3 | 19. -7π/3 | 20. -2π |
| 21. -5π/3 | 22. -4π/3 | 23. -π | 24. -2π/3 |
| 25. -π/3 | 26. 0 | 27. π/3 | 28. 2π/3 |
| 29. π |
В правильной шестиугольной призме \(ABCDEFA_1B_1C_1D_1E_1F_1\) сторона основания \(AB\) равна 6, а боковое ребро \(AA_1\) равно \(5\sqrt3\). На ребре \(DD_1\) отмечена точка \(M\) так, что \(DM:MD_1=2:3\). Плоскость \(\alpha\) параллельна прямой \(A_1F_1\) и проходит через точки \(M\) и \(B\).
а) Докажите, что сечение призмы \(ABCDEFA_1B_1C_1D_1E_1F_1\) плоскостью \(\alpha\) - равнобедренная трапеция.
б) Найдите объём пирамиды, вершиной которой является точка \(A_1\), а основанием - сечение призмы \(ABCDEFA_1B_1C_1D_1E_1F_1\) плоскостью \(\alpha\).
Решите неравенство \(\left(5\cdot 0{,}2^{x+0{,}5}-0{,}2\cdot5^{x+0{,}5}\right)\left(0{,}5\log^2_{0{,}2}(x+0{,}5)-2\log_5(x+0{,}5)\right)>0\).
15 января планируется взять кредит в банке на 3 года. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей.
Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 22,5°. Точка P лежит вне прямоугольника, а угол BPC равен 135°.
а) Докажите, что углы BCP и POB равны.
б) Прямая PO пересекает сторону AD в точке F. Найдите DF, если BP=7 и CP=5√2.
Найдите все значения \(a\), при каждом из которых среди корней уравнения \(x^2-10x+35=a|x-6|\) будет ровно два положительных.
У Коли в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 25 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 30 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая.
а) Может ли у Коли быть 50 монет?
б) Какое наибольшее количество монет может быть у Коли?
в) Какая наибольшая сумма рублей может быть у Коли?
Введите ответ в форме строки "да;123;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.