36 вариантов ЕГЭ 2023
Меню курса
35 вариант ЕГЭ Ященко 2023
Решение 35 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Один из углов прямоугольного треугольника равен 66°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.
В сборнике билетов по физике всего 25 билетов, в 11 из них встречается вопрос по теме "Конденсаторы". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме "Конденсаторы".
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов. Известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,5. Найдите отношение вероятностей событий "стрелок поразит ровно пять мишеней" и "стрелок поразит ровно три мишени".
Найдите корень уравнения \(\log_{3}{(x+6)}=\log_{3}{(10-x)}-1 \)
Найдите значение выражения \(\dfrac{(5\sqrt{3})^2}{10}\)
Прямая \(y=8x+11\) параллельна касательной к графику функции \(y=x^2+7x-7\). Найдите абсциссу точки касания.
Рейтинг R интернет-магазина вычисляется по формуле \(R=r_{пок}-\dfrac{r_{пок}-r_{экс}}{(K+1)^m}\), где \(m=\dfrac{0{,}02K}{r_{пок}+0{,}1}\), \(r_{пок}\) – средняя оценка магазина покупателями, \(r_{экс}\) – оценка магазина, данная экспертами, \(K\) – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,3, а оценка экспертов равна 0,38.
Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час позже автомобилиста. Ответ дайте в км/ч.
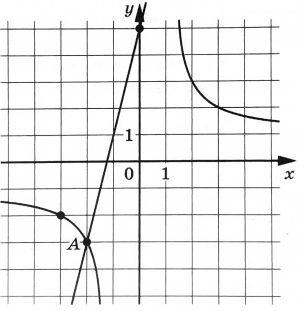
На рисунке изображены графики функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках \(A(-2;-3)\) и \(B(x_0;y_0)\). Найдите \(x_0\).
Найдите точку минимума функции \(y=\dfrac{162}{x}+2x+7\)
а) Решите уравнение \(2\cos^4x+3\sin^2x-2=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-\dfrac{5\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
Основанием пирамиды FABC является правильный треугольник ABC со стороной 36. Все боковые рёбра пирамиды равны 30. На рёбрах FB и FC отмечены соответственно точки K и N так, что BK=CN=20. Через точки K и N проведена плоскость α, перпендикулярная плоскости ABC.
а) Докажите, что плоскость α делит медиану AM в отношении 2:7.
б) Найдите расстояние от точки B до плоскости α.
Решите неравенство \(\log^2_{0{,}2}{(x-3)^8}+8\log_{5}{(x-3)^4}\leqslant32\)
15 декабря планируется взять кредит в банке на сумму 600 тысяч рублей на n+1 месяц. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
- 15-го числа n-го месяца долг составит 200 тысяч рублей;
- к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен. Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 852 тысячи рублей.
В треугольнике \(ABC\) известно, что \(AC=10\) и \(AB=BC=14\).
а) Докажите, что средняя линия треугольника, параллельная стороне \(AC\), пересекает окружность, вписанную в треугольник \(ABC\).
б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне \(AC\).
Ответ запишите в виде несократимого отношения без пробелов, например "4:13:5".
Найдите все значения \(a\), при каждом из которых неравенство \((4|x|-a-3)(x^2-2x-2-a)\leqslant0 \) имеет хотя бы одно решение на промежутке \([-4;4]\).
Группу детей можно перевезти автобусами модели А или автобусами модели Б. Известно, что в автобусе модели А количество мест больше 30, но меньше 40, а в автобусах модели Б — больше 40, но меньше 50. Если всех детей рассадить в автобусы модели А, то все места будут заняты. Если всех детей рассадить в автобусы модели Б, то все места также будут заняты, но потребуется на один автобус меньше.
а) Может ли потребоваться 5 автобусов модели А?
б) Найдите наименьшее возможное количество детей в группе, если известно, что их больше 150.
в) Найдите наибольшее возможное количество детей в группе.
Введите ответ в форме строки "да;123;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.