36 вариантов ЕГЭ 2023
Меню курса
30 вариант ЕГЭ Ященко 2023
Решение 30 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
В треугольнике ABC средняя линия DE параллельна стороне AB. Найдите площадь треугольника ABC, если площадь трапеции ABED равна 48.
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находится уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах.
В чемпионате по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающих первым, окажется из Индии.
За круглый стол на 6 стульев в случайном порядке рассаживаются 4 мальчика и 2 девочки. Найдите вероятность того, что обе девочки не будут сидеть рядом.
Найдите корень уравнения \((x-11)^4=(x+3)^4 \)
Найдите значение выражения \(\dfrac{(\sqrt{20}+\sqrt{12})^2}{4+\sqrt{15}}\)
Материальная точка движется прямолинейно по закону \(x(t)=\frac{1}{2}t^3-2t^2+6t+25 \), где \(x\) – расстояние от точки отсчёта в метрах, \(t\) - время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t = 4\).
Водолазный колокол, содержащий \(\nu=2\) моля воздуха при давлении \(p_1=2{,}4\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_2\) в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле \(A=a\nu T\log_{2}{\dfrac{p_2}{p_1}} \), где \(a=13{,}5 \dfrac{Дж}{моль \cdot К}\) - постоянная, \(T=300 \,К\) - температура воздуха. Найдите, какое давление \(p_2\) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в \(16200 Дж\). Ответ дайте в атмосферах.
Первая труба заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая труба заполняет резервуар объёмом 396 литров. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба?
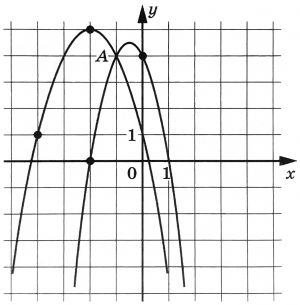
На рисунке изображены графики функций \(f(x)=-2x^2-2x+4\) и \(g(x)=ax^2+bx+c\), которые пересекаются в точках \(A(-1;4)\) и \(B(x_0;y_0)\). Найдите \(x_0\).
Найдите точку минимума функции \(y=(x+8)^2\cdot e^{-x-3} \)
а) Решите уравнение \(\cos{2x}\sin{2x}\sin{\frac{2\pi}{3}}=\dfrac{1}{4}\cos{\left(8x-\frac{3\pi}{2} \right)} \)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[\frac{8\pi}{3};\frac{10\pi}{3} \right] \)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. πn/4, n∈Z | 2. π/12+πn/2, n∈Z | 3. 5π/24+πn/2, n∈Z | 4. 3π/8+πn/2, n∈Z |
| 5. -π/12+πn/2, n∈Z | 6. -5π/24+πn/2, n∈Z | 7. -3π/8+πn/2, n∈Z |
б)
| 8. 8π/3 | 9. 65π/24 | 10. 11π/4 | 11. 67π/24 |
| 12. 17π/6 | 13. 23π/8 | 14. 3π | 15. 19π/6 |
| 16. 25π/8 | 17. 77π/24 | 18. 13π/4 | 19. 79π/24 |
| 20. 10π/3 |
Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Решите неравенство \(30\cdot 3^{\log_{2}{(7-x)}}+3^{1+\log_{2}{x}}-3^{\log_{2}{(7x-x^2)}}\geqslant 90 \)
Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает p человек, то каждый из них получает в сутки 200p руб. Если на втором объекте работает p человек, то каждый из них получает в сутки (50p+300) руб. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?
Введите ответ в форме строки "5;15;30000", где на 1 первом месте количество человек на 1 объекте, на 2 месте - на 2 объекте, на 3 месте - наименьшая зарплата.
На сторонах AC, AB, BC прямоугольного треугольника ABC с прямым углом C во внешнюю сторону построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно
а) Докажите, что LC - высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC=10
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} \log_{11}{(a - y^2)}=\log_{11}{(a - x^2)}\\x^2+y^2=2x+6y\end{cases} \) имеет ровно два различных решения.
Для набора 40 различных натуральных чисел выполнено, что сумма любых двух чисел из этого набора меньше суммы любых четырёх чисел из этого набора.
а) Может ли одним из этих чисел быть число 777?
б) Может ли одним из этих чисел быть число 33?
в) Какое наименьшее значение может принимать сумма чисел этого набора?
Введите ответ в форме строки "да;нет;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.