36 вариантов ЕГЭ 2023
Меню курса
20 вариант ЕГЭ Ященко 2023
Радиус окружности, вписанной в ромб, равен 1,5. Найдите сторону ромба, если один из его углов равен 30°.

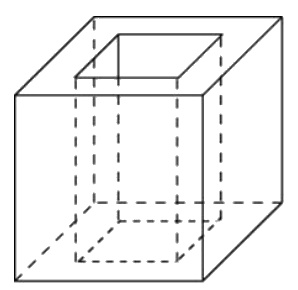
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,6 и боковым ребром 1. Найдите площадь полной поверхности получившейся фигуры.
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 2, но не дойдя до отметки 11.
В группе туристов 15 человек, в том числе три друга - Юра, Боря и Егор. Группу случайным образом разбивают на три равные подгруппы. Найдите вероятность того, что все трое окажутся в разных подгруппах. Ответ округлите до сотых.
Решите уравнение \(\sin{\dfrac{\pi(2x+7)}{6}}=-\dfrac{\sqrt{3}}2\). В ответе запишите наибольший отрицательный корень.
Найдите 5(4p(x+2)-p(4x)), если p(x)=x-2.
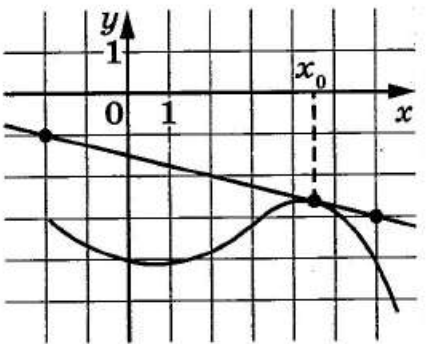
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\)
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \(A(\omega)=\dfrac{A_0\omega_p^2}{\vert \omega_p^2-\omega^2 \vert} \), где \( \omega \) – частота вынуждающей силы (в \(с^{−1}\)), \(A_0\) – постоянный параметр, \( \omega_p=330\, с^{-1}\) – резонансная частота. Найдите максимальную частоту \( \omega\), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на 80%. Ответ дайте в \(с^{−1}.\)
Расстояние между городами A и B равно 84 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 65 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
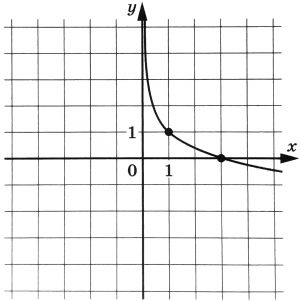
На рисунке изображен график функции \(f(x)=b+\log_ax\). Найдите значение \(x\), при котором \(f(x)=-2\)
Найдите наименьшее значение функции \(y=(x+4)^2e^{-4-x}\) на отрезке [-5;-3].
а) Решите уравнение \(36\log^2_{\frac{1}{8}}{x}+4\log_{\frac{1}{4}}{x}-5=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5;5].
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
В правильной треугольной призме ABCA₁B₁C₁ точки K и N - соответственно середины ребер AA₁ и AC. Плоскость \(\alpha\) проходит через точки K и N параллельно прямой CB₁.
а) Докажите, что сечением призмы ABCA₁B₁C₁ плоскостью \(\alpha\) является равнобедренная трапеция.
б) Найдите угол между прямой CC₁ и плоскостью \(\alpha\), если AB=4, AA₁=√3.
Решите неравенство \(4\cdot 9^{1-\frac{5}{x}}-91\cdot 12^{-\frac{5}{x}}+3\cdot 4^{2-\frac{10}{x}}\geqslant 0\)
В июле 2023 года планируется взять кредит на 12 лет в размере 1200 тыс. рублей. Условия его возврата таковы:
- каждый январь с 2024 по 2029 год долг возрастает на 18% по сравнению с концом предыдущего года;
- каждый январь с 2030 по 2035 год долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Точка K лежит на отрезке AB. Прямая, проходящая через точку B, касается окружности с диаметром AK в точке N и второй раз пересекает окружность с диаметром BK в точке M. Продолжение отрезка NK пересекает окружность с диаметром BK в точке P.
а) Докажите, что прямые AN и BP параллельны.
б) Найдите площадь треугольника AKP, если BM=1 и MN=4.
Найдите все значения \(a\), при каждом из которых уравнение \((7x-6)\cdot \ln(x+a)=(7x-6)\cdot \ln(4x-a)\) имеет ровно один корень на отрезке [0;1].
На доске написано более 35, но менее 49 целых чисел. Среднее арифметическое этих чисел равно 5, среднее арифметическое всех положительных из них равно 14, а среднее арифметическое всех отрицательных из них равно -7.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше, положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Введите ответ в форме строки "11;п;1234". Где ответы на пункты разделены ";", и второй ответ "п", если положительных или "о", если отрицательных.