36 вариантов ЕГЭ 2023
Меню курса
32 вариант ЕГЭ Ященко 2023
Решение 32 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
В четырёхугольник ABCD вписана окружность, АВ=8, ВС=5 и CD=27. Найдите четвёртую сторону четырёхугольника.
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 27√2. Найдите площадь боковой поверхности конуса.
При производстве в среднем на каждые 1500 насосов приходится 36 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер достанут третьим по счету?
Найдите корень уравнения \(0{,}2^{5+4x}=125\).
Найдите значение выражения \(\left(3\dfrac{1}{8}-1{,}5\right):\dfrac{1}{56}\).
На рисунке изображён график \(y = f'(x)\) производной функции \(f(x)\), определённой на интервале \((-3; 8)\). В какой точке отрезка \([-2; 3]\) функция \(f(x)\) принимает наименьшее значение?

В телевизоре ёмкость высоковольтного конденсатора \(C=5\cdot10^{-6}\,Ф\). Параллельно с конденсатором подключён резистор с сопротивлением \(R=6\cdot10^{6}\,Ом\). Во время работы телевизора напряжение на конденсаторе \(U_0=34 кВ\). После выключения телевизора напряжение на конденсаторе убывает до значения \(U \,(кВ)\) за время, определяемое выражением \(t=\alpha RC\log_{2}{\dfrac{U_0}{U}}\) (с), где \(\alpha=1{,}7\) - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошла 51 с. Ответ дайте в киловольтах.
Плиточник должен уложить 120 м² плитки. Если он будет укладывать на 8 м² в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
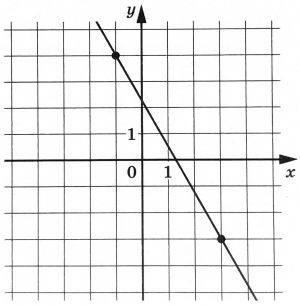
На рисунке изображен график функции \(f(x)=kx+b\). Найдите значение \(x\), при котором \(f(x)=-20{,}5\)
Найдите точку максимума функции \(y=x^{3}+18x^{2}+81x+23\).
а) Решите уравнение \(2\sin^2x-3\sqrt3\sin\left(\dfrac{\pi}{2}+x\right)-5=0\)
б) Укажите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{5\pi}{2};-\pi \right] \).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
В правильной четырёхугольной пирамиде SABCD сторона основания АВ равна 4, а боковое ребро SA равно 5. На ребре SC отмечена точка K, причём SK:KC = 1:3. Плоскость \(\alpha\) содержит точку K и параллельна плоскости SAD.
а) Докажите, что сечение пирамиды SABCD плоскостью \(\alpha\) — трапеция.
б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD плоскостью \(\alpha\).
Решите неравенство \(\log_{2}{(18-9x)}-\log_{2}{(x+2)}>\log_{2}{(x^2-6x+8)}\)
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму в рублях планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей?
(Считайте, что округления при вычислении платежей не производятся.)
Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E.
а) Докажите, что углы ∠EOC=∠ECO.
б) Найдите площадь треугольника ACE, если радиус описанной около треугольника ABC окружности равен 6√3, ∠ABC=60°.
Найдите все значения \(a\), при каждом из которых уравнение \(\dfrac{|x-6|+a-6}{x^2-10x+a^2}=0\) имеет ровно два различных корня.
В ящике лежит 58 овощей, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей, масса каждого из которых меньше 1000 г, равна 976 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1036 г.
а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г?
б) Могло ли в ящике оказаться ровно 12 овощей, масса каждого из которых равна 1000 г?
в) Какую наименьшую массу может иметь овощ в этом ящике?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.