19 вариант ЕГЭ Ященко 2023

Сторона ромба равна 10, острый угол равен 30°. Найдите радиус окружности, вписанной в ромб.

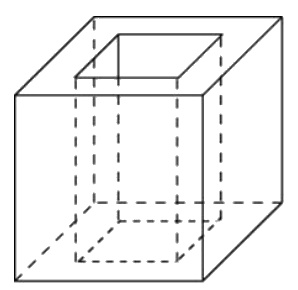
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,4 и боковым ребром 1. Найдите площадь полной поверхности получившейся фигуры.

​

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 10.

В классе 26 учащихся, среди них три подружки – Оля, Аня и Юля. Класс случайным образом разбивают на 2 равные группы. Найдите вероятность того, что все три девочки окажутся в одной группе.

Решите уравнение \(\mathrm{tg}\dfrac{\pi(2x+5)}{6}=\sqrt{3}\). В ответе запишите наибольший отрицательный корень.

Найдите \(\dfrac{g(10-x)}{g(10+x)}\), если \(g(x)=\sqrt[3]{x(20-x)}\), при \(|x|≠10\)

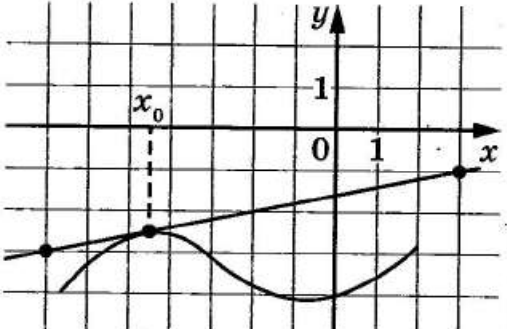
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\)

Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \(A(\omega)=\dfrac{A_0\omega_p^2}{\vert \omega_p^2-\omega^2 \vert} \), где \(\omega\) – частота вынуждающей силы (в \(с^{−1}\)), \(A_0\) – постоянный параметр, \(\omega_p=345\, с^{-1}\) – резонансная частота. Найдите максимальную частоту \(\omega\), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на 12,5%. Ответ дайте в \(с^{−1}.\)

Расстояние между городами A и B равно 180 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

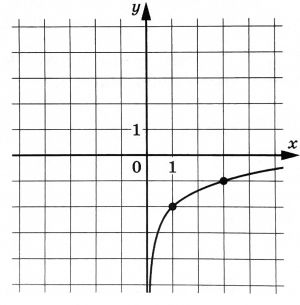
На рисунке изображен график функции \(f(x)=b+\log_ax\). Найдите \(f(81)\)

Найдите точку максимума функции \(y=(x+35)e^{35-x}\)

а) Решите уравнение \(16\log^2_9x+4\log_{\frac13}x-3=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5;5]

В правильной треугольной призме ABCA₁B₁C₁ точка K - середина ребра AA₁, а AB=AA₁. Плоскость \(\alpha\) проходит через точки K и B₁ параллельно прямой BC₁.
а) Докажите, что плоскость \(\alpha\) делит ребро A₁C₁ в отношении 1:2.
б) Найдите расстояние от точки A₁ до плоскости \(\alpha\), если AB=6.

В ответ запишите квадрат этого расстояния.

Решите неравенство \(25\cdot4^{\frac12-\frac2{x}}-133\cdot10^{-\frac2{x}}+4\cdot5^{1-\frac4{x}}\leqslant0\)

В июле 2025 года планируется взять кредит в банке на сумму 650 тыс. рублей на 10 лет. Условия его возврата таковы:
- в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
- в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита. Ответ дайте в тысячах рублей.

В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM прямые.
а) Докажите, что BM=CM.
б) Найдите угол ABC, если угол BCD равен 64°, а расстояние от точки M до прямой BC равно стороне AD.

Найдите все значения параметра \(a\), при каждом из которых уравнение \(\sqrt{5-7x}\ln(9x^2-a^2)=\sqrt{5-7x}\ln(3x+a)\) имеет ровно один корень.

На доске написано 11 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 8, среднее арифметическое семи наибольших из них равно 14.
а) Может ли наибольшее из этих одиннадцати чисел равняться 16?
б) Может ли среднее арифметическое всех одиннадцати чисел равняться 10?
в) Найдите наименьшее значение среднего арифметического всех одиннадцати чисел.

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а в ответе на пункт в) сумма этих чисел.