36 вариантов ЕГЭ 2024
Меню курса
11 вариант ЕГЭ Ященко 2024
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.

Даны векторы \(\vec{a}(6;-1)\), \(\vec{b}(-5;-2)\) и \(\vec{c}(-3;5)\). Найдите длину вектора \(\vec{a}-\vec{b}+\vec{c}\)
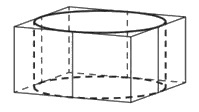
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объем параллелепипеда.
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810г равна 0,96. Вероятность того, что масса окажется больше, чем 790г, равна 0,93. Найдите вероятность того, что масса буханки окажется больше, чем 790г, но меньше, чем 810г.
Найдите корень уравнения \(\log_3(5-2x)=\log_3(1-4x)+1\)
Найдите значение выражения \(\dfrac{\sin126°}{4\sin63°\cdot\sin27°}\)
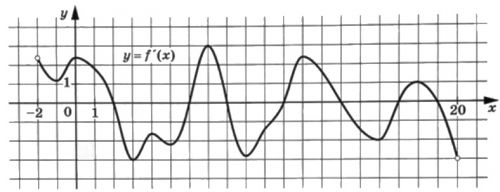
На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (-2;20). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [1;15].
При адиабетическом процессе для идеального газа выполняется закон \(pV^k=1{,}3122\cdot10^7\,Па\cdot м^4\), где \(p\) – давление в газе в паскалях, \(V\) – объем газа в кубических метрах, \(k=\dfrac43\). Найдите, какой объем \(V\) (в куб. м) будет занимать газ при давлении \(p\), равном \(1{,}25\cdot10^6\,Па\)
Моторная лодка прошла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
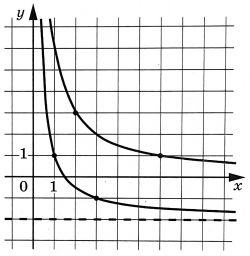
На рисунке изображены части графиков функций \(f(x)=\dfrac{k}{x}\) и \(g(x)=\dfrac{c}{x}+d\). Найдите ординату точки перечесения графиков этих функций.
Найдите наименьшее значение функции \(y=x\sqrt{x}-27x+6\) на отрезке [1;422]
а) Решите уравнение \(2\sin^2x-3\cos(-x)-3=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[2\pi;\dfrac{7\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали трапеции пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD=9, BC=7, SO=6, а прямая SO перпендикулярна прямой AD.
Решите неравенство \(4^x+\dfrac{112}{4^x-32}\leqslant0\)
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– платежи в 2028 и 2029 годах должны быть равными;
– к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE=CE.
а) Докажите, что AL:AC=AB:BC.
б) Найдите EL, если AC=21, tg∠BCA=0,4.
Найдите все значения \(a\), при каждом из которых уравнение \((a-x)^2+4a+1=(2x+1)^2-8|x|\) имеет четыре различных корня.
Есть три коробки: в первой коробке 112 камней, во второй – 99 камней, а третья – пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй – 99, а в третьей – 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее количество камней могло оказаться в третьей коробке?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.