36 вариантов ЕГЭ 2024
Меню курса
9 вариант ЕГЭ Ященко 2024
Основания трапеции равны 29 и 44. Найдите отрезок, соединяющий середины диагоналей трапеции.
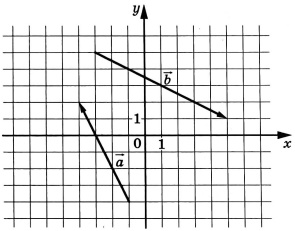
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите \(\cos\alpha\), где \(\alpha\) - угол между векторами \(\vec{a}\) и \(\vec{b}\)
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 6√2. Найдите площадь боковой поверхности конуса.
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые три дня по 11 докладов, остальные распределены поровну между четвертым и пятым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
Ваня бросил игральный кубик, и у него выпало больше 2 очков. Петя бросил игральный кубик, и у него выпало меньше 6 очков. Найдите вероятность того, что у Пети выпало очков больше, чем у Вани.
Решите уравнение \(\sqrt{3-2x}=2x+3\). Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Найдите значение выражения \(\dfrac{\left(2^{\frac47}\cdot5^{\frac23}\right)^{21}}{10^{12}}\)
Материальная точка движется прямолинейно по закону \(x(t)=t^2+7t+13\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 25 м/с?
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону \(U=U_0\cos{(ωt+\varphi)}\), где \(t\) – время в секундах, амплитуда \(U_0=2\,В\), частота \(ω=120°/с\), фаза \(\varphi=-45°\). Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Имеется два сосуда. Первый содержит 60 кг, а второй - 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 76% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 82% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
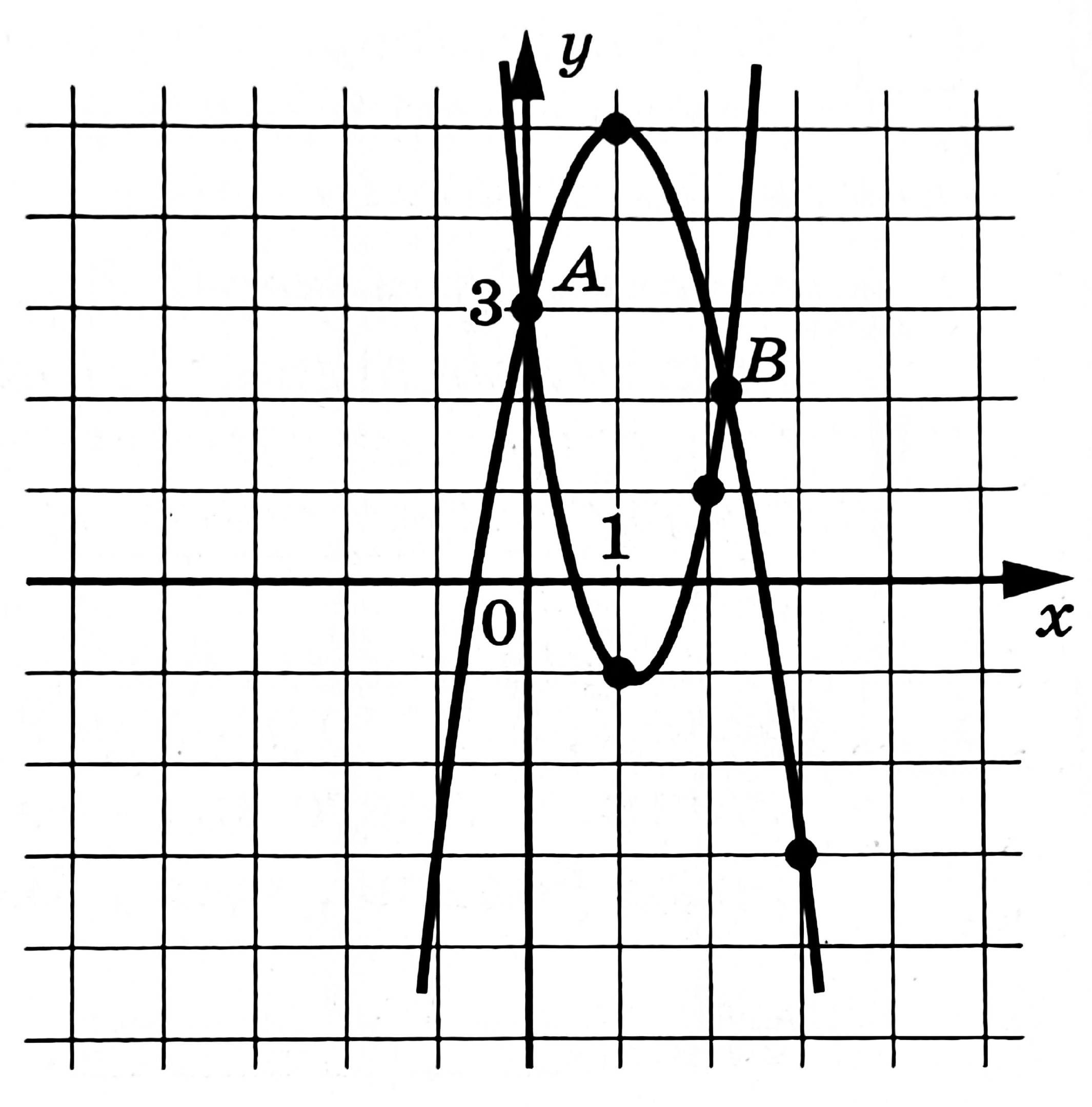
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=-2x^2+4x+3\), которые пересекаются в точках \(A(0;3)\) и \(B(x_B;y_B)\). Найдите \(y_B\).
Найдите наименьшее значение функции \(y=2x^2-5x+\ln x-3\) на отрезке \(\left[\dfrac16;\dfrac76\right]\)
а) Решите уравнение \(4\log_2^2(\sin x)-3\log_{0{,}5}(\sin^2x)+2=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
Основанием четырёхугольной призмы ABCDA₁B₁C₁D₁ является прямоугольная трапеция ABCD, в которой ∠BAD=90°, а основания AB и CD соответственно равны c и b.
а) Докажите, что если c=4b, то объёмы многогранников, на которые призму ABCDA₁B₁C₁D₁ делит плоскость CDA₁, относятся как 3:2.
б) Объёмы многогранников DA₁D₁CB₁C₁ и ADA₁BCB₁, на которые призму ABCDA₁B₁C₁D₁ делит плоскость CDA₁, соответственно равны 30 и 20. Найдите высоту призмы ABCDA₁B₁C₁D₁, если CD=5, а AD=4.
Решите неравенство \(6^{2x^2-5|x|}\cdot5^{3|x|}\leqslant1\)
В сентябре 2027 года Михаил планирует взять кредит в банке на 6 лет в размере 1500 тыс. рублей. Условия его возврата таковы:
- в январе 2028, 2029 и 2030 годов долг увеличивается на r% от суммы долга на конец предыдущего года;
- в январе 2031, 2032 и 2033 годов долг увеличивается на (r+3)% от суммы долга на конец предыдущего года;
- в период с февраля по август необходимо выплатить часть долга;
- в сентябре каждого года действия кредита долг должен быть на одну и ту же сумму меньше долга на сентябрь предыдущего года;
- к сентябрю 2033 года кредит должен быть полностью погашен.
Найдите r, если общая сумма выплат по кредиту должна составить 2175 тыс. рублей.
В равнобедренной трапеции ABCD боковая сторона AB равна a, а основание AD=c больше основания BC=b. Построена окружность, касающаяся сторон AB, CD и AD.
а) Докажите, что если b+c>2a, то окружность пересекает сторону BC в двух точках.
б) Найдите длину той части отрезка BC, которая находится внутри окружности, если c=12, b=10, a=8.
Найдите все значения \(a\), при каждом из которых уравнение \(\sqrt{15-2x-x^2}=3a|x|+a-3ax-x\) имеет ровно один корень.
Дано четырёхзначное число \(\overline{abcd}\), где a, b, c и d - соответственно цифры разрядов тысяч, сотен, десятков и единиц, причём a≠0.
а) Может ли произведение a·b·c·d быть больше суммы a+b+c+d в 3 раза?
б) Цифры a, b, c и d попарно различны. Сколько существует различных чисел \(\overline{abcd}\) таких, что a·b·c·d
в) Известно, что a·b·c·d=k(a+b+c+d), где k - двузначное число. При каком наименьшем значении \(\overline{abcd}\) число k будет наибольшим?
Введите ответ в форме строки "да;45;14". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.