36 вариантов ЕГЭ 2024
Меню курса
32 вариант ЕГЭ Ященко 2024
В треугольнике АВС высота СН равна 6, АВ=ВС, АС=8. Найдите синус угла АСВ.
Даны векторы \(\vec{a}(-6;2)\) и \(\vec{b}(9;13)\). Найдите косинус угла между векторами \(\vec{a}\) и \(\vec{b}\)
В правильной треугольной призме ABCA₁B₁C₁ все рёбра которой равны 2, найдите угол между прямыми BB₁ и AC₁. Ответ дайте в градусах.
Всего в группе туристов 21 человек, в том числе Лёня и Ваня. Группу случайным образом делят на три подгруппы по 7 человек для посадки в три микроавтобуса. Какова вероятность того, что Лёня и Ваня случайно окажутся в одном микроавтобусе?
Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,16. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения \(\dfrac1{5x-14}=\dfrac1{4x-3}\)
Найдите значение выражения \(\dfrac{{{\log }_9 32\ }}{{{\log }_{27} 0{,}5\ }}\)
На рисунке изображён график функции \(y= f(x)\), определённой на интервале \((-5; 9)\). Найдите количество решений уравнения \(f ' (x)=0\) на отрезке \([-2; 8]\).

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a = 6500 \,км/ч^2\). Скорость \(v\) (в км/ч) вычисляется по формуле \(v=\sqrt{2la}\), где \(l\) — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 130 км/ч.
Теплоход проходит по течению реки до пункта назначения 416 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 21 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 50 часов. Ответ дайте в км/ч.
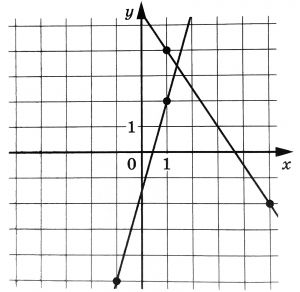
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Найдите точку максимума функции \(y=\left(5x-6\right)\cos x-5\sin x\ -8\), принадлежащую промежутку \(\left(0;\dfrac{\pi }{2}\right)\)
а) Решите уравнение \(\cos2x - \sqrt{2}\cos \Big(\dfrac{3\pi}{2} + x\Big) – 1 = 0\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\Big[\dfrac{3\pi}{2}; 3\pi\Big]\).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых ребер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA – высота пирамиды.
б) Найдите угол между прямыми SC и BD.
Решите неравенство \(x^2\log_{243} (-x-3)\geqslant \log_3 (x^2+6x+9)\)
В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы:
– каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей;
– выплаты в 2026 и 2027 годах равны;
– к июлю 2027 года долг будет выплачен полностью.
Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.
Две окружности разных радиусов касаются внешним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите ВС, если радиусы окружностей равны √15 и 15.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} \sqrt{a-y^2}=\sqrt{a-x^2} \\ x^2+y^2=2x+4y \end{cases}\) имеет ровно два различных решения.
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 1, к каждому числу из второй группы - цифру 8, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 4 раза?
б) Могла ли сумма всех этих чисел увеличиться в 18 раз?
в) Сумма всех этих чисел увеличилась в 11 раз. Какое наибольшее количество чисел могло быть написано на доске?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.