36 вариантов ЕГЭ 2024
Меню курса
25 вариант ЕГЭ Ященко 2024
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
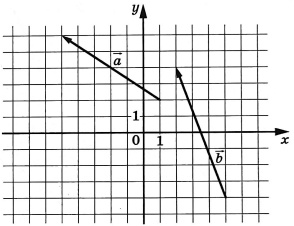
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите координаты вектора \(\vec{c}\), если \(\vec{c}=0{,}5\vec{b}-\vec{a}\). В ответ запишите сумму координат вектора \(\vec{c}\)
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решите уравнение \(\sqrt{9-8x}=-x\). Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Найдите значение выражения \(\dfrac{2^{\log_93}}{2^{\log_9243}}\)
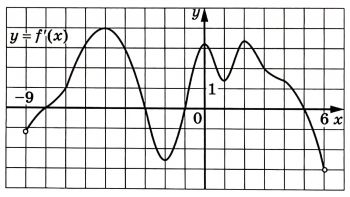
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Груз массой 0,25 кг колеблется на пружине. Его скорость \(v\) меняется по закону \(v = v_0 \cos\dfrac{2\pi t}{T}\), где \(t\) – время с момента начала колебаний, \(T= 2\) с – период колебаний, \(v_0= 1{,}6\) м/с. Кинетическая энергия \(E\) (в джоулях) груза вычисляется по формуле \(E = \dfrac{mv^2}{2}\), где \(m\) – масса груза в килограммах, \(v\) – скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
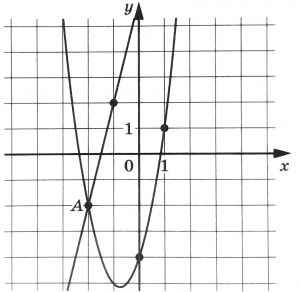
На рисунке изображены графики функций \(f(x)=ax^2+bx+c\) и \(g(x)=kx+d\), которые пересекаются в точках А и B. Найдите абсциссу точки B.
Найдите наибольшее значение функции \( y=x^5+5x^3-140x \) на отрезке \(\left[-8;-1\right]\)
а) Решите уравнение \(\sin{2x}+\cos{2x}=1\).
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right] \).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
В правильной призме ABCDA₁B₁C₁D₁ с основанием ABCD боковое ребро равно \(\sqrt{3}\) , а сторона основания равна 2. Через точку А₁ перпендикулярно плоскости AB₁D₁ проведена прямая \(l\).
а) Докажите, что прямая \(l\) пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми \(l\) и СВ₁.
Решите неравенство \( 7^{\log_{\frac{1}{7}}{\log_{\frac{1}{2}}{\left(-x\right)}}}< 2^{\log_{\frac{1}{2}}{\log_{\frac{1}{7}}{\left(-x\right)}}} \)
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
- в январе 2026, 2027 и 2028 годов долг возрастает на 20% по сравнению с концом предыдущего года;
- в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Около окружности с центром O описана трапеция ABCD с основаниями AD и BC.
а) Докажите, что ∠AOB=∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB=CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет 12/49 площади трапеции ABCD.
Найдите все такие значения \(a\), при каждом из которых неравенство \(-1\leqslant\sin x(a-\cos2x)\leqslant1\) верно при всех действительных значениях \(x\).
Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.