36 вариантов ЕГЭ 2024
Меню курса
15 вариант ЕГЭ Ященко 2024
Стороны AB, BC, CD и AD четырехугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 46°, 115°, 122°, 77°. Найдите угол ABC. Ответ дайте в градусах.
Даны векторы \(\vec{a}(-1;3)\), \(\vec{b}(4;1)\) и \(\vec{c}(2;c_0)\). Найдите \(c_0\), если \((\vec{a}+\vec{b})\cdot\vec{c}=0\)
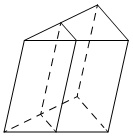
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0,097. В некотором городе из 1000 проданных принтеров в течение года в мастерские по гарантии поступила 101 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Вероятность того, что батарейка бракованная, равна 0,03. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решите уравнение \(\log_42^{8x+20}=8\)
Найдите значение выражения \(\dfrac{\sqrt[3]6\cdot\sqrt[3]{12}}{\sqrt[3]9}\)
Прямая \(y=5x-8\) является касательной к графику функции \(y=6x^2+bx+16\). Найдите \(b\), учитывая, что абсцисса точки касания больше 0.
Двигаясь со скоростью v=4 м/с, трактор тащит сани с силой F=90 кН, направленной под острым углом α к горизонту. Мощность, развиваемая трактором, вычисляется по формуле N=F·v·cosα. Найдите, при каком угле α (в градусах) эта мощность будет равна 180 кВт (кВт – это кН·м/с).
Расстояние между пристанями А и В равно 144 км. Из А в В по течению реки отправился плот, а через 1 час за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому моменту времени плот проплыл 18 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 1 км/ч. Ответ дайте в км/ч.
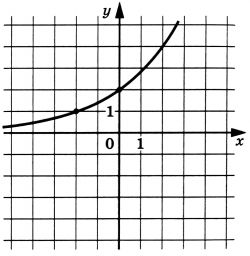
На рисунке изображен график функции \(f(x)=a^{x+2}\). Найдите \(f(6)\).
Найдите наименьшее значение функции \(y=x^3+18x^2+81x+56\) на отрезке [-7;0]
а) Решите уравнение \(2^{5\sin5x}+6^{1+\sin5x}=24^{\sin5x}+3\cdot8^{\frac13+\sin5x}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}2;\dfrac{7\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. πn/2, n∈Z | 2. πn/3, n∈Z | 3. πn/4, n∈Z | 4. πn/5, n∈Z |
б)
| 5. 5π/2 | 6. 13π/5 | 7. 8π/3 | 8. 11π/4 |
| 9. 14π/5 | 10. 17π/6 | 11. 3π | 12. 19π/6 |
| 13. 16π/5 | 14. 13π/4 | 15. 10π/3 | 16. 17π/5 |
В правильную треугольную пирамиду с боковым ребром √13 и стороной основания 6 вписан шар. Плоскость α перпендикулярна высоте пирамиды и проходит через её середину.
а) Докажите, что плоскость α и шар пересекаются более, чем в одной точке.
б) Найдите площадь сечения шара плоскостью α.
Решите неравенство \(\dfrac{\log^2_3(x-1{,}5)-1}{2^x-3}\leqslant0\)
В июне 2025 года Вадим Олегович планирует взять кредит в банке на 4 года. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 10% от суммы долга на конец предыдущего года;
– в период с февраля по июнь каждого из 2026, 2027 и 2028 годов необходимо выплатить часть долга, причём каждый из платежей 2027 и 2028 годов в 1,5 раза больше платежа предыдущего года;
– в период с февраля по июнь 2029 года выплачивается оставшаяся сумма по кредиту, равная 3304840 рублей.
Найдите сумму кредита, если общие выплаты по нему составили 10904840 рублей.
В трапеции ABCD с меньшим основанием BC точки E и F – середины сторон BC и AD соответственно. В каждый из четырехугольников ABEF и ECDF можно вписать окружность.
а) Докажите, что трапеция ABCD равнобедренная.
б) Найдите радиус окружности, описанной около трапеции ABCD, если AB=7, а радиус окружности вписанной в четырехугольник ABEF, равен 2,5.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}y^2-x=4-2a\\y^4+x^2=a^2-3a+4\end{cases}\) имеет ровно два различных решения.
Из k кг материала фабрика изготавливает n одинаковых деталей массой m кг каждая, причем k=nm+q, где q кг – остатки материала, и q < m. После внедрения новых технологий на фабрике начали выпускать детали нового типа, каждая из которых стала на 0,2 кг легче детали старого типа, причем из 63 кг материала деталей нового типа стали делать на две больше, чем делали деталей старого типа из 64 кг материала.
а) Может ли новая деталь весить столько, что на изготовление 15 новых деталей будет достаточно 63 кг материала, а на 16 – уже нет?
б) Может ли новая деталь весить столько, что на изготовление 40 новых деталей будет достаточно 63 кг материала, а на 41 – уже нет?
в) Найдите такое минимальное число n, что фабрика может выпускать n новых деталей из 80 кг материала, а n-1 деталь не сможет, не нарушая условия q < m.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.