33 вариант ЕГЭ Ященко 2024

В четырехугольник ABCD вписана окружность, AB=13, CD=18. Найдите периметр четырехугольника ABCD.

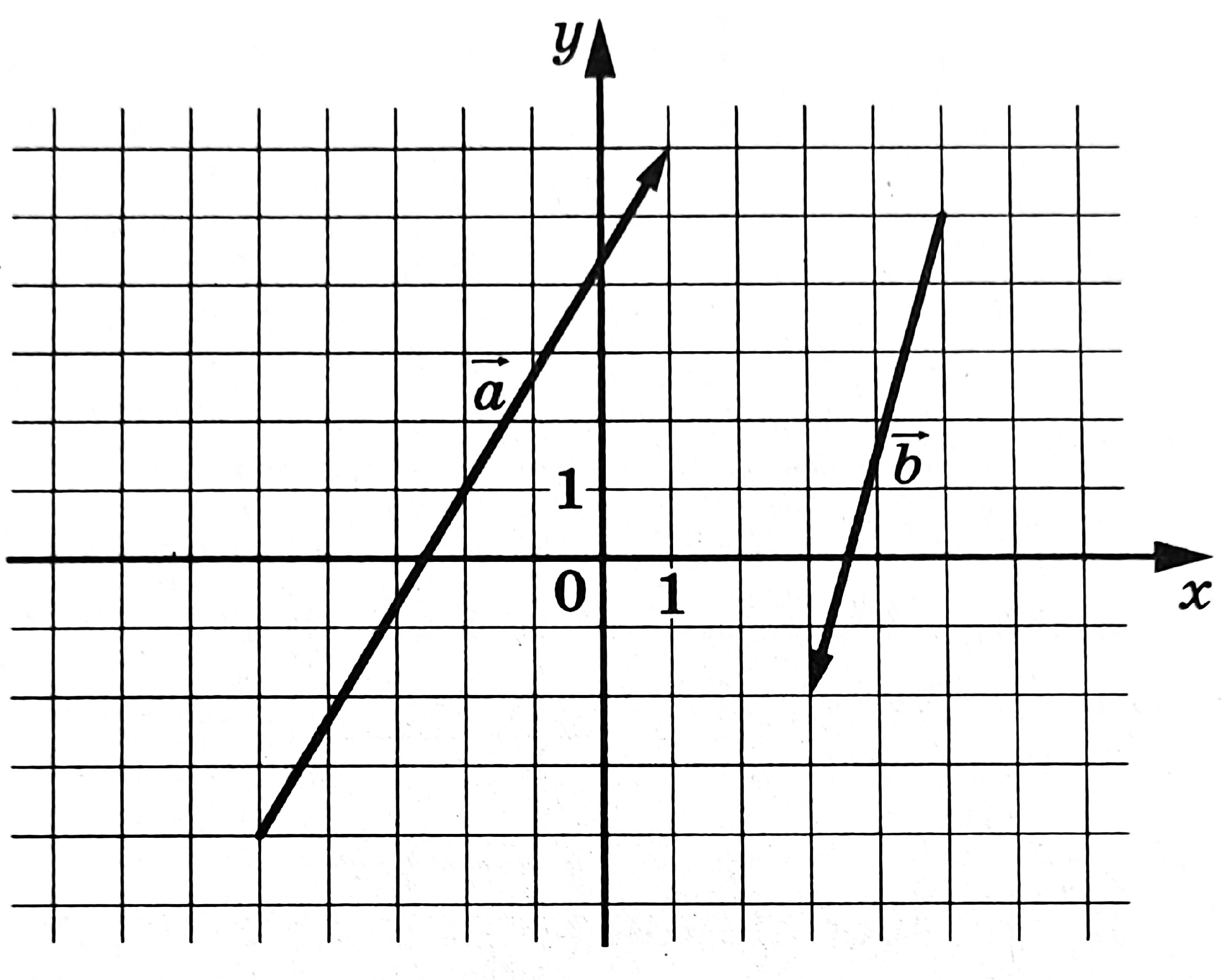
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите длину вектора \(2\vec{b}-\vec{a}\)

Радиусы двух шаров равны 7 и 24. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

В гонке с раздельным стартом участвуют 25 лыжников, среди которых 7 спортсменов из Норвегии. Порядок старта определяется с помощью жребия случайным образом. Один из норвежских лыжников получил стартовый номер «5». Найдите вероятность, что он будет стартовать за своим соотечественником.

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 95% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 45% яиц высшей категории. Всего высшую категорию получает 60% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Найдите корень уравнения \(\log_3(2-x)=\log_9{16}\)

Найдите значение выражения \(\dfrac{8^{2{,}8}\cdot 5^{3{,}2}}{20^{2{,}2}}\)

На рисунке изображён график функции \(y=f(x)\), определенной на интервале \((-4;9)\). Определите количество целых точек, в которых производная функции положительна.

Небольшой мячик бросают под острым углом \(\alpha\) к плоской горизонтальной поверхности земли. Максимальная высота полета мячика \(H\) (в м) вычисляется по формуле \(H=\dfrac{v^2_0}{4g}(1-\cos2\alpha)\), где \(v_0=12\,м/с\) – начальная скорость мячика, а \(g\) – ускорение свободного падения (считайте \(g=10\, м/с^2\)) При каком наименьшем значении угла \(\alpha\) мячик пролетит над стеной высотой \(4{,}4\,м\) на расстоянии \(1\,м\)? Ответ дайте в градусах.

Имеется два сплава. Первый содержит 50% никеля, второй — 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

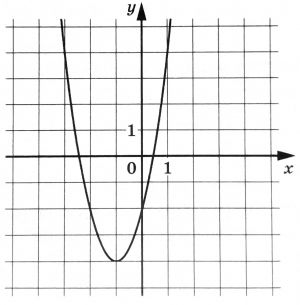
На рисунке изображен график функции \(f(x)=2x^2+bx+c\), где числа \(b\) и \(c\) – целые. Найдите \(f(-5)\).

Найдите наибольшее значение функции \(y=3x^5-5x^3+16\) на отрезке \([-4;0]\)

а) Решите уравнение \((x^2+2x-1)\left( \log_2(x^2-3)+\log_{0{,}5}(\sqrt3-x)\right)=0\)
​б) Найдите все корни этого уравнения, принадлежащие отрезку \([-2{,}5; -1{,}5]\).

В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно √21. На ребрах AB и SB отмечены точки M и K соответственно, причем AM=4, SK:KB=1:3.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объем пирамиды BCKM.

Решите неравенство \(\dfrac{4^{x-0{,}5}+1}{9\cdot 4^x-16^{x+{0{,}5}}-2}\leqslant 0{,}5\)

Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1806000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено в таблице.

На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?

В четырехугольнике ABCD противоположные стороны не параллельны. Дианогали четырехугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин – точка O.
а) Докажите, что около четырёхугольника ABCD можно описать окружность.
б) Найдите радиус вписанной окружности, если AC=10, BD=26.

Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} \dfrac5{x}+3-y=\left| y-2+\dfrac3{x}\right| \\ 2y(y-4)+3x(ax+4)=xy(2a+3)\end{cases}\) имеет более трех решений.

Петя участвовал в викторине по истории. За каждый правильный ответ участнику начисляется 8 баллов, за каждый неверный – списывается 8 баллов, за отсутствие ответа списывается 3 балла. По результатам викторины Петя набрал 35 баллов.
а) На сколько вопросов Петя не дал ответа, если в викторине было 30 вопросов?
б) На сколько вопросов Петя не дал ответа, если в викторине было 35 вопросов?
в) На сколько вопросов Петя ответил правильно, если в викторине было 33 вопроса?

Введите ответ в форме строки "21;43;7", где ответы на пункты разделены ";".