36 вариантов ЕГЭ 2024
Меню курса
4 вариант ЕГЭ Ященко 2024
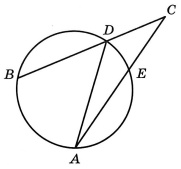
Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 116° и 38°. Ответ дайте в градусах.
Даны векторы \(\vec{a}(4;-1)\) и \(\vec{b}(b_0;8)\). Найдите \(b_0\), если \(|\vec{b}|=2{,}5|\vec{a}|\). Если таких значений несколько, в ответ запишите большее из них.
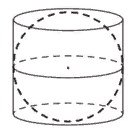
Шар вписан в цилиндр. Площадь поверхности шара равна 25. Найдите площадь полной поверхности цилиндра.
В группе туристов 30 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 3 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Ш. полетит вторым рейсом вертолёта.
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3 орла»?
Найдите корень уравнения \(2{,}5^{2-3x}=0{,}16^{2x}\)
Найдите \(45\cos2\alpha\), если \(\cos\alpha=-0{,}9\)
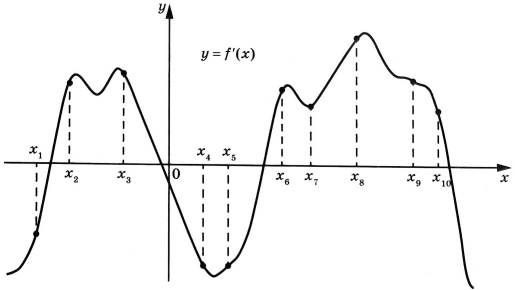
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\). На оси абсцисс отмечено десять точек: \(x_1, x_2, ..., x_{10}\). Сколько из этих точек принадлежат промежуткам возрастания функции \(f(x)\)?
В телевизоре ёмкость высоковольтного конденсатора \(C=2\cdot10^{-6}\,Ф\). Параллельно с конденсатором подключён резистор с сопротивлением \(R=6\cdot10^{6}\,Ом\). Во время работы телевизора напряжение на конденсаторе \(U_0=10\, кВ\). После выключения телевизора напряжение на конденсаторе убывает до значения \(U \,(кВ)\) за время, определяемое выражением \(t=\alpha RC\log_{2}{\dfrac{U_0}{U}}\) (с), где \(\alpha=0{,}7\) - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 16,8 с. Ответ дайте в киловольтах.
На изготовление 40 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 70 деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
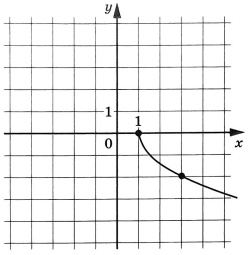
На рисунке изображен график функции \(f(x)=p\sqrt{x+d}\). Найдите значение \(x\), при котором \(f(x)=-6\)
Найдите точку минимума функции \(y=(x+9)^2(x+3)+7\)
а) Решите уравнение \(4\sqrt3\sin^3x=\cos\left(2x+\dfrac{3\pi}2\right)\)
б) Найдите все его корни, принадлежащие отрезку \(\left[\dfrac{9\pi}2;6\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 9π/2 | 18. 14π/3 | 19. 19π/4 | 20. 29π/6 |
| 21. 5π | 22. 31π/6 | 23. 21π/4 | 24. 16π/3 |
| 25. 11π/2 | 26. 17π/3 | 27. 23π/4 | 28. 35π/6 |
| 29. 6π |
Основанием правильной треугольной пирамиды PABC является треугольник ABC, AP:AB=3:4. На апофеме грани BCP отметили точку K, которая делит эту апофему в отношении 1:4, считая от точки P. Через точки A и K параллельно прямой BC проведена плоскость α.
а) Докажите, что плоскость α перпендикулярна апофеме грани BCP.
б) Найдите угол между прямой AC и плоскостью α.
Решите неравенство \(|\log_9(2x+1)^2-1|-|\log_3(1-x)-3|\geqslant1\)
В октябре 2027 года Борис планирует взять кредит в банке на 7 лет в размере 2560 тыс. рублей. Условия его возврата таковы:
- в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
- в период с февраля по сентябрь необходимо выплатить часть долга;
- в октябре каждого года в первые пять лет действия кредита (2028-2032 гг.) долг должен быть на одну и ту же величину Q рублей меньше долга на октябрь предыдущего года;
- в 2033 и 2034 годах выплаты по кредиту равны;
- к октябрю 2034 года кредит должен быть полностью погашен.
Найдите величину Q, если общая сумма выплат по кредиту должна составлять 4168 тыс. рублей.
В прямоугольный треугольник ABC с прямым углом A вписана окружность с центром в точке O и радиусом R. К этой окружности параллельно прямой AB проведена касательная, которая пересекает стороны BC и AC в точках D и E соответственно. В треугольник CDE вписана окружность с центром в точке O₁ и радиусом r. Прямые OO₁ и AB пересекаются в точке P.
а) Докажите, что AP:PB=cos∠ACB
б) Найдите площадь треугольника ABC, если R=5, r=3.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}x^2+y^2=|2{,}7a|\\y=a(x-a)\end{cases}\) имеет ровно два различных решения.
Трёхзначное число A имеет k натуральных делителей (в том числе 1 и A).
а) Может ли k быть равно 15?
б) Может ли k быть равно 28?
в) Найдите все числа A, для которых k⩾30.
Введите ответ в форме строки "да;да;1;2;34", где ответы на пункты разделены ";", и первые два ответа с маленькой буквы, а числа в пункте В по возрастанию.