8.1. Геометрический смысл производной (Задачи ЕГЭ профиль)

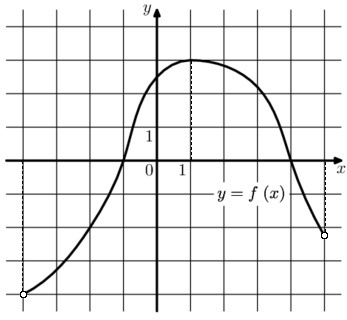
На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечено восемь точек \(x_1, \ldots, x_8\). Сколько среди этих точек таких, производная в которых отрицательна?

На рисунке изображён график функции \(y=f(x)\), определённой на интервале \((-9 ; 5)\). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

На рисунке изображён график функции \(y=f(x)\), определённой на интервале \((-5; 9)\). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

На рисунке изображен график функции \(f(x)\), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

На рисунке изображен график функции \(f(x)\), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

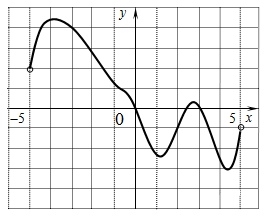
На рисунке изображён график функции \(y=f(x)\), определённой на интервале (-9;5). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

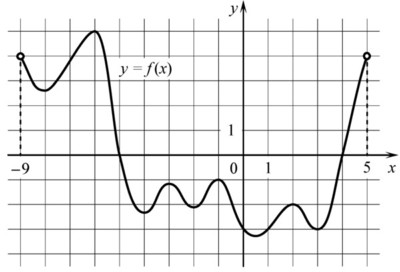
На рисунке изображён график дифференцируемой функции \(y=f(x)\). На оси абсцисс отмечены девять точек: \(x_{1}, x_{2}, ..., x_{9}\). Найдите все отмеченные точки, в которых производная функции \(f(x)\) отрицательна. В ответе укажите количество этих точек.
​

На рисунке изображён график функции \(y=f(x)\), определённой на интервале (-2;12). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

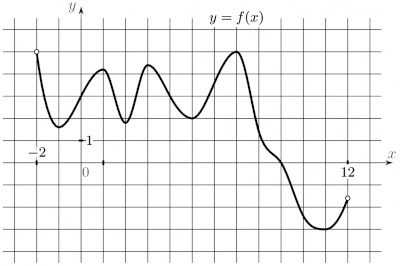
На рисунке изображен график функции \(y = f(x)\) и восемь точек на оси абсцисс: \(x_{1}\), \(x_{2}\), \(x_{3}\), \(x_{4}\), \(x_{5}\), \(x_{6}\), \(x_{7}\), \(x_{8}\). В скольких из этих точек производная функции \(f(x)\) отрицательна?

На рисунке изображён график дифференцируемой функции \(y=f(x)\), определённой на интервале \((-4;5)\). Найдите точку из отрезка \([-2;4]\), в которой производная функции \(f(x)\) равна 0.