36 вариантов ЕГЭ 2025
Меню курса
1 вариант ЕГЭ Ященко 2025
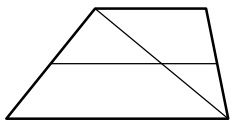
Средняя линия трапеции равна 24. Одна из диагоналей трапеции делит среднюю линию в отношении 2:3. Найдите большее основание трапеции.
Даны векторы \(\vec{a}(16;-0{,}4)\) и \(\vec{b}(2;5)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 48. Найдите объём цилиндра.

Термометр измеряет температуру в помещении. Вероятность того, что температура окажется ниже +18°С, равна 0,27. Вероятность того, что температура окажется выше +21°С, равна 0,36. Найдите вероятность того, что температура в помещении окажется в промежутке от +18°С до +21°С.
Стрелок стреляет по трём мишеням. Вероятность попадания в мишень первым выстрелом равна 0,5. Если стрелок промахнулся, он может выстрелить по мишени второй раз. Вероятность попадания в мишень вторым выстрелом равна 0,6. Найдите вероятность того, что стрелок поразит ровно одну мишень из трёх.
Найдите корень уравнения \(\left(\dfrac14\right)^{1-3x}=2^{x+2}\)
Найдите значение выражения \(\log_{2{,}5}4-\log_{2{,}5}10\)
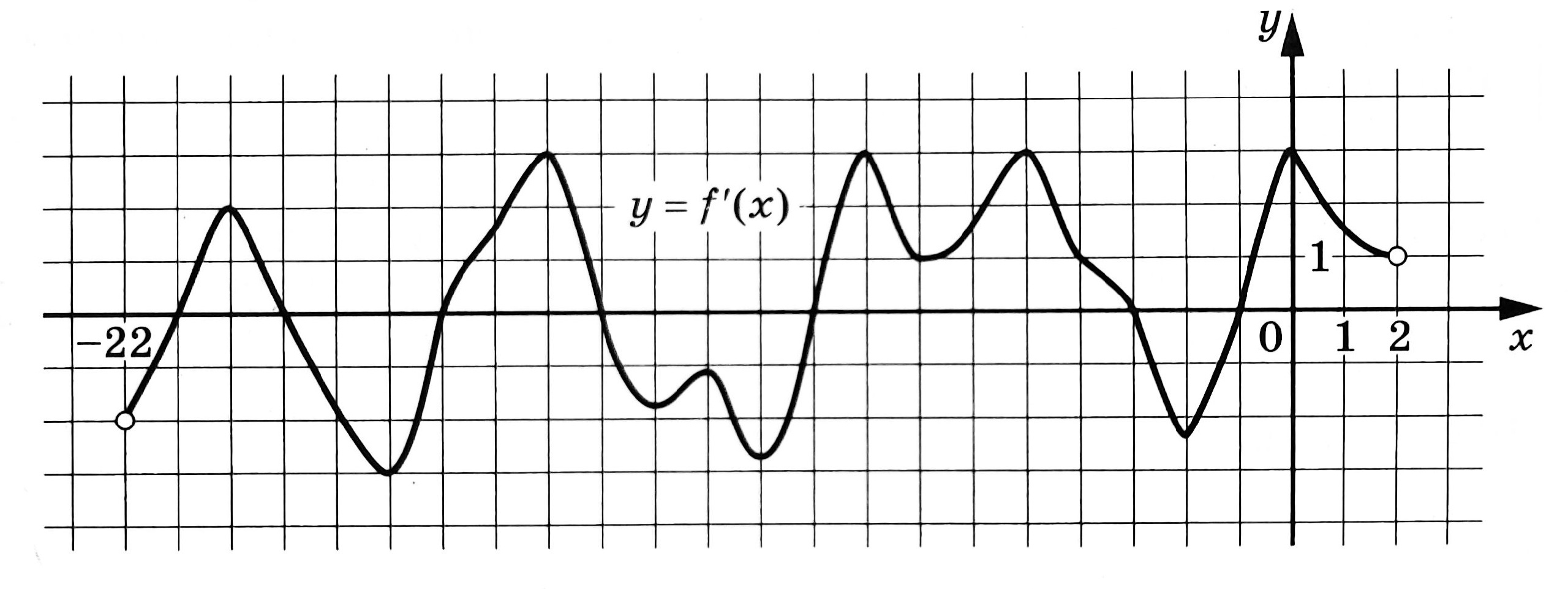
На рисунке изображён график y=f'(x) - производной функции f(x), определённой на интервале (-22;2). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-18;1].
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a\) км/ч². Скорость вычисляется по формуле \(v=\sqrt{2la}\), где \(l\) — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,9 км, приобрести скорость 150 км/ч. Ответ выразите в км/ч².
Расстояние между пристанями A и B равно 160 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 38 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
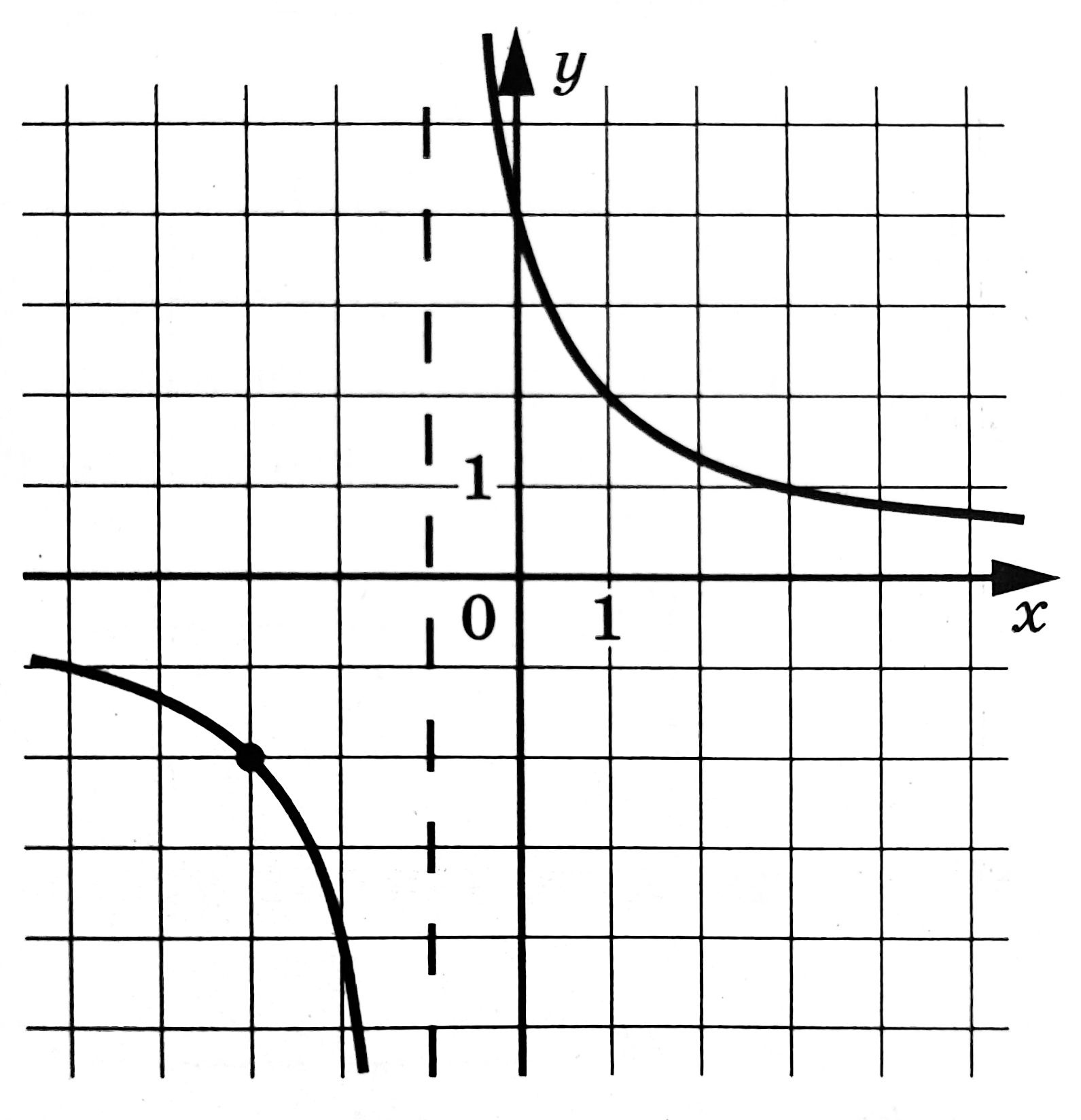
На рисунке изображён график функции \(f(x)=\dfrac{k}{x+a}\). Найдите значение \(x\), при котором \(f(x)=20\).
Найдите точку минимума функции \(y=(x+13)^2\cdot e^{6-x}\)
а) Решите уравнение \(\sin^4\dfrac{x}4-\cos^4\dfrac{x}4=\cos\left(x-\dfrac{3\pi}2\right)\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-4\pi;-\pi\right]\)
В правильной треугольной пирамиде SABC с основанием ABC точки D и E делят соответственно рёбра AC и SB так, что AD:DC=SE:EB=1:2. На продолжении ребра SC за точку S отмечена точка O. Прямые OD и OE пересекают рёбра AS и BC в точках P и F соответственно, причём BF=FC.
a) Докажите, что отрезки DE и PF пересекаются.
б) Найдите отношение AP:PS.
Решите неравенство \(16\cdot5^{1-\frac8{x}}-189\cdot 20^{-\frac4{x}}+25\cdot 2^{2-\frac{16}{x}}\leqslant0\)
В июле 2026 года планируется взять кредит в банке на некоторую сумму на 4 года. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить 312500 рублей.
Какую сумму (в рублях) планируется взять в кредит, если он будет полностью погашен этими четырьмя платежами?
Окружность с центром в точке O вписана в ромб ABCD и касается его сторон AB, CD и AD соответственно в точках F, K и P.
a) Докажите, что прямая FP параллельна диагонали ромба BD.
б) Найдите длину диагонали BD, если известно, что FP=12 и PK=5.
Найдите все значения \(a\), при каждом из которых площадь фигуры, ограниченной линиями \(y=\dfrac{a}2x+2a\) и \(y=a|x|+|a|\), будет меньше 7, но не меньше 3.
На координатной прямой отмечены целые числа. Митя играет в следующую игру: фишка стоит на отметке 0; Митя бросает игральный кубик и сдвигает фишку на выпавшее число очков вправо (положительное направление прямой), если выпадает чётное число очков, и влево (отрицательное направление прямой), если выпадает нечётное число очков. Через некоторое время Митя закончил игру.
a) Может ли фишка оказаться на отметке «-50», если Митя 30 раз бросил кубик?
б) Известно, что чётное число очков выпадало столько же раз, сколько и нечётное число очков. Какое наименьшее число бросков кубика понадобится, чтобы фишка оказалась на отметке «-50»?
в) Известно, что чётное число очков выпадало столько же раз, сколько и нечётное число очков. Какое наименьшее число бросков кубика понадобится, чтобы фишка оказалась на отметке «-55», если также известно, что при бросании кубика каждая грань выпадала хотя бы один раз, но любые две грани не выпадали одинаковое количество раз?
Введите ответ в форме строки "да;12;34". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.