36 вариантов ЕГЭ 2025
Меню курса
3 вариант ЕГЭ Ященко 2025
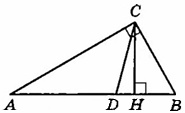
Острый угол B прямоугольного треугольника ABC равен 67°. Найдите угол между высотой CH и биссектрисой CD, проведёнными из вершины прямого угла. Ответ дайте в градусах.
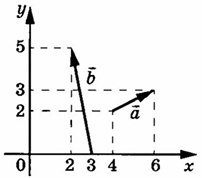
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите длину вектора \(5\vec{b}-\vec{a}\)
Площадь большого круга шара равна 12. Найдите площадь поверхности шара.

В классе 21 учащийся, среди них два друга – Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
По условиям лотереи каждый пятый билет является выигрышным. Какое наименьшее количество билетов нужно купить, чтобы среди них с вероятностью больше, чем 0,5 оказался выигрышный билет?
Найдите корень уравнения \(\left(1-x^2\right)^3=-27\). Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Найдите значение выражения \(7\cdot\sqrt[5]{256}\cdot\sqrt[20]{256}\)
Прямая y=7x+11 параллельна касательной к графику функции y=x²+8x+6. Найдите абсциссу точки касания.
Водолазный колокол, содержащий в начальный момент времени \(\nu=2\) моля воздуха объёмом \(V_1=18\) л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма \(V_2\). Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле \(A=a\nu T\log_2{\frac{V_1}{V_2}}\), где \(a=9{,}15\) Дж/моль⋅К - постоянная, а \(T=300\) К — температура воздуха. Найдите, какой объём \(V_2\) (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 10980 Дж.
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 12 рабочих, во второй 15 рабочих. Через 9 дней после начала работы в первую бригаду перешли 6 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
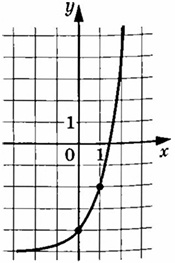
На рисунке изображен график функции \(f(x)=a^x+b\). Найдите значение \(x\), при котором \(f(x)=76\)
Найдите наибольшее значение функции \(y=\ln(5x)-5x-5\) на отрезке [0,1;0,5]
а) Решите уравнение \(2\sin^2\left(\dfrac{x}2-\dfrac{\pi}{4}\right)\cdot\sin^2\left(\dfrac{x}2+\dfrac{\pi}{4}\right)=\cos^4x\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-3\pi;-2\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π |
Решите неравенство \(2^x\cdot\log_3x+3^x\log_2x\leqslant2\cdot3^{x-1}\log_3x+3\cdot2^{x-1}\log_2x\)
В мае 2027 планируется взять кредит в банке на сумму 1400 тыс. рублей на 8 лет. Условия его возврата таковы:
- в январе 2028, 2029, 2030 и 2031 годов долг возрастает на 17% по сравнению с концом предыдущего года;
- в январе 2032, 2033, 2034 и 2035 годов долг возрастает на 14% по сравнению с концом предыдущего года;
- с февраля по апрель каждого года необходимо выплатить часть долга;
- в мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года;
- к маю 2035 года кредит должен быть полностью погашен.
На сколько рублей последняя выплата будет меньше выплаты 2030 года?
В параллелограмме ABCD с острым углом BAD точка E - середина стороны BC. Через точку B перпендикулярно прямой AB и через точку E перпендикулярно прямой DE проведены соответственно две прямые, которые пересекаются в точке K.
а) Докажите, что AK=KD.
б) Найдите угол BAD, если расстояние от точки К до прямой AD равно длине oтрезка EC и ∠CED=58°. Ответ дайте в градусах.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}|x|-|y|=a\\x-1=\sqrt{y+4}\end{cases}\) имеет ровно два различных решения.
Есть 60 карточек, на каждой из которых написано натуральное число больше 1. Все числа различные. На обратной стороне каждой карточки ставят цветовую отметку: если число делится на 3 – красную, если на 4 – синюю, если на 5 – зелёную. Получилось так, что на каждой карточке ровно две цветовые отметки.
а) Какое наибольшее количество карточек может быть с числами меньше 200?
б) Получилось, что на 20 карточках есть синяя и зелёная отметки, на 20 карточках есть синяя и красная отметки, на 20 карточках есть красная и зелёная отметки. Найдите наименьшее возможное значение наибольшего числа среди чисел, указанных на карточках.
в) Получилось, что на 45 карточках синяя отметка. Найдите наименьшее возможное значение наибольшего числа среди указанных на карточках.
Введите ответ в форме строки "21;43;7", где ответы на пункты разделены ";"