36 вариантов ЕГЭ 2025
Меню курса
4 вариант ЕГЭ Ященко 2025
Острый угол B прямоугольного треугольника ABC равен 36°. Найдите угол между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла. Ответ дайте в градусах.
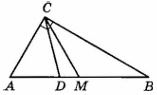
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите длину вектора \(6\vec{a}-\vec{b}\)
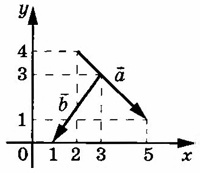
Даны два шара. Радиус первого в 1,8 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
В классе 26 учащихся, среди них два друга – Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в разных группах.
По условиям лотереи выигрышных билетов в ней всего на 20% меньше, чем билетов без выигрыша. Какое наименьшее количество билетов нужно купить, чтобы среди них с вероятностью больше, чем 0,75 оказался выигрышный билет?
Найдите корень уравнения \(\left(5-x^2\right)^4=256\). Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Прямая y=9x-5 является касательной к графику функции y=x²+7x+c. Найдите c.
Водолазный колокол, содержащий \(\nu=13\) молей воздуха при давлении \(p_1=1{,}2\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_2\) (в атмосферах). Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле \(A=a\nu T\log_{2}{\dfrac{p_2}{p_1}}\), где \(a=15\frac{Дж}{моль \cdot К}\) - постоянная, \(T=300\,К\) - температура воздуха. Найдите, какое давление \(p_2\) (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 117000 Дж.
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 12 рабочих, во второй 21 рабочий. Через 10 дней после начала работы в первую бригаду перешли 12 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
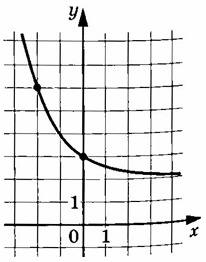
На рисунке изображен график функции \(f(x)=a^x+b\). Найдите \(f(-4)\)
Найдите точку минимума функции \(y=5x-\ln(x+4)^5+9\)
а) Решите уравнение \(3\cos^2\left(\dfrac{x}2+\dfrac{\pi}{4}\right)\cdot\cos^2\left(\dfrac{x}2-\dfrac{\pi}{4}\right)=\cos^4x\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([3\pi;4\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π | 18. 19π/6 | 19. 13π/4 | 20. 10π/3 |
| 21. 7π/2 | 22. 11π/3 | 23. 15π/4 | 24. 23π/6 |
| 25. 4π |
В правильной призме ABCDEFA₁B₁C₁D₁E₁F₁ на ребре CC₁ отметили точку K так, что CK:KC₁=4:1. Через точки K и D₁ параллельно прямой DF₁ провели плоскость α.
а) Докажите, что плоскость α пересекает ребро B₁C₁ в его середине.
б) Найдите угол между плоскостями AFF₁ и α, если AB=4, AA₁=15. Ответ дайте в градусах.
Решите неравенство \(3^x\cdot\log_5x+5^x\log_3x>3\cdot5^{x-1}\log_5x+5\cdot3^{x-1}\log_3x\)
В июне 2028 планируется взять кредит на 10 лет в размере 1500 тыс. рублей на 8 лет. Условия его возврата таковы:
- каждый январь с 2029 по 2033 год долг возрастает на 22% по сравнению с концом предыдущего года;
- каждый январь с 2034 по 2038 год долг возрастает на 18% по сравнению с концом предыдущего года;
- с февраля по май каждого года необходимо выплатить часть долга;
- в июне каждого года долг должен быть на одну и ту же величину меньше долга на июнь предыдущего года;
- к июню 2038 года кредит должен быть полностью погашен.
На сколько рублей последняя выплата будет меньше выплаты 2033 года?
В параллелограмме ABCD с острым углом BAD точка E - середина стороны BC. Через точку B перпендикулярно прямой AB и через точку E перпендикулярно прямой DE проведены соответственно две прямые, которые пересекаются в точке K.
а) Докажите, что AK=KD.
б) Найдите угол ADE, если расстояние от точки К до прямой AD равно длине oтрезка EC и ∠ADC=110°. Ответ дайте в градусах.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}|x|-|y|=a\\x-4=\sqrt{9-y}\end{cases}\) имеет ровно два различных решения.
Есть 60 карточек, на каждой из которых написано натуральное число больше 1. Все числа различные. На обратной стороне каждой карточки ставят цветовую отметку: если число делится на 3 – красную, если на 4 – синюю, если на 5 – зелёную. Получилось так, что на каждой карточке поставлено не менее двуч цветовыех отметок.
а) Какое наибольшее количество карточек может быть с числами меньше 200?
б) Получилось, что на k карточках только синяя и зелёная отметки, на k карточках - только синяя и красная, на k карточках - только красная и зелёная. Найдите наименьшее возможное значение наибольшего числа среди чисел, указанных на карточках.
в) Карточек с двумя отметками, одна из которых синяя, получилось 37. Найдите наименьшее возможное значение наибольшего числа среди указанных на карточках.
Введите ответ в форме строки "21;43;7", где ответы на пункты разделены ";"