2 вариант ЕГЭ Ященко 2025

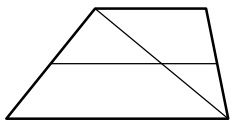
Средняя линия трапеции равна 30. Одна из диагоналей трапеции делит среднюю линию в отношении 5:3. Найдите меньшее основание трапеции.

Даны векторы \(\vec{a}(-8;0{,}5)\) и \(\vec{b}(5;24)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)

Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 72. Найдите объём конуса.

В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется синей, равна 0,47, а того, что она окажется красной, равна 0,18. Найдите вероятность того, что ручка окажется чёрной.

Стрелок стреляет по трём мишеням. Вероятность попадания в мишень первым выстрелом равна 0,4. Если стрелок промахнулся, он может выстрелить по мишени второй раз. Вероятность попадания в мишень вторым выстрелом равна 0,5. Найдите вероятность того, что стрелок поразит ровно две мишени из трёх.

Найдите корень уравнения \(4^{x-2}=\left(\dfrac12\right)^{3x+1}\)

Найдите значение выражения \(\log_{0{,}2}100-\log_{0{,}2}4\)

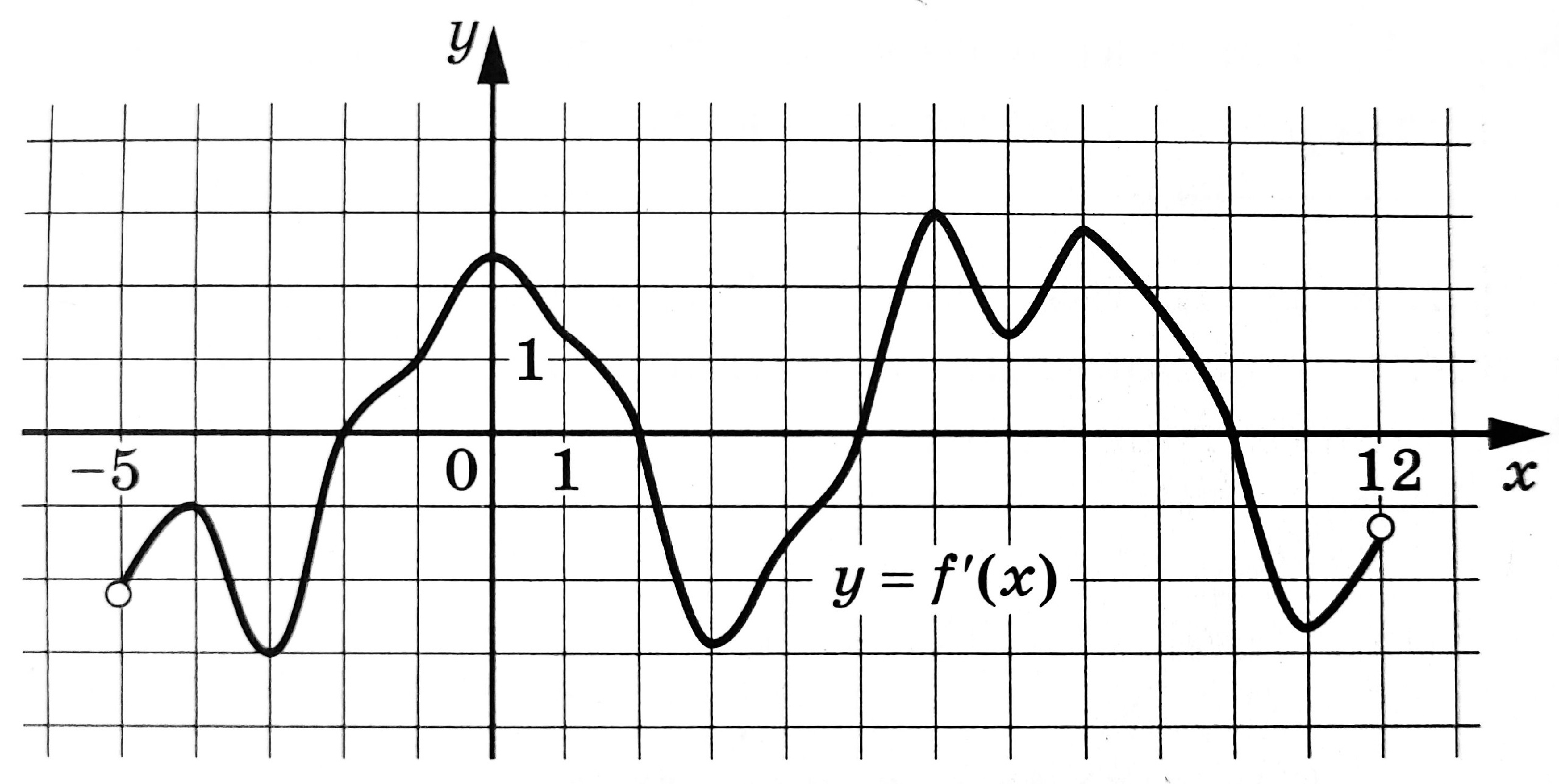
На рисунке изображён график y=f'(x) - производной функции f(x), определённой на интервале (-5;12). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-4;9].

​

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a=6250 \,км/ч^2\). Скорость \(v\) (в км/ч) вычисляется по формуле \(v=\sqrt{2la}\), где \(l\) - пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.

Расстояние между пристанями A и B равно 72 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 3 км/ч. Ответ дайте в км/ч.

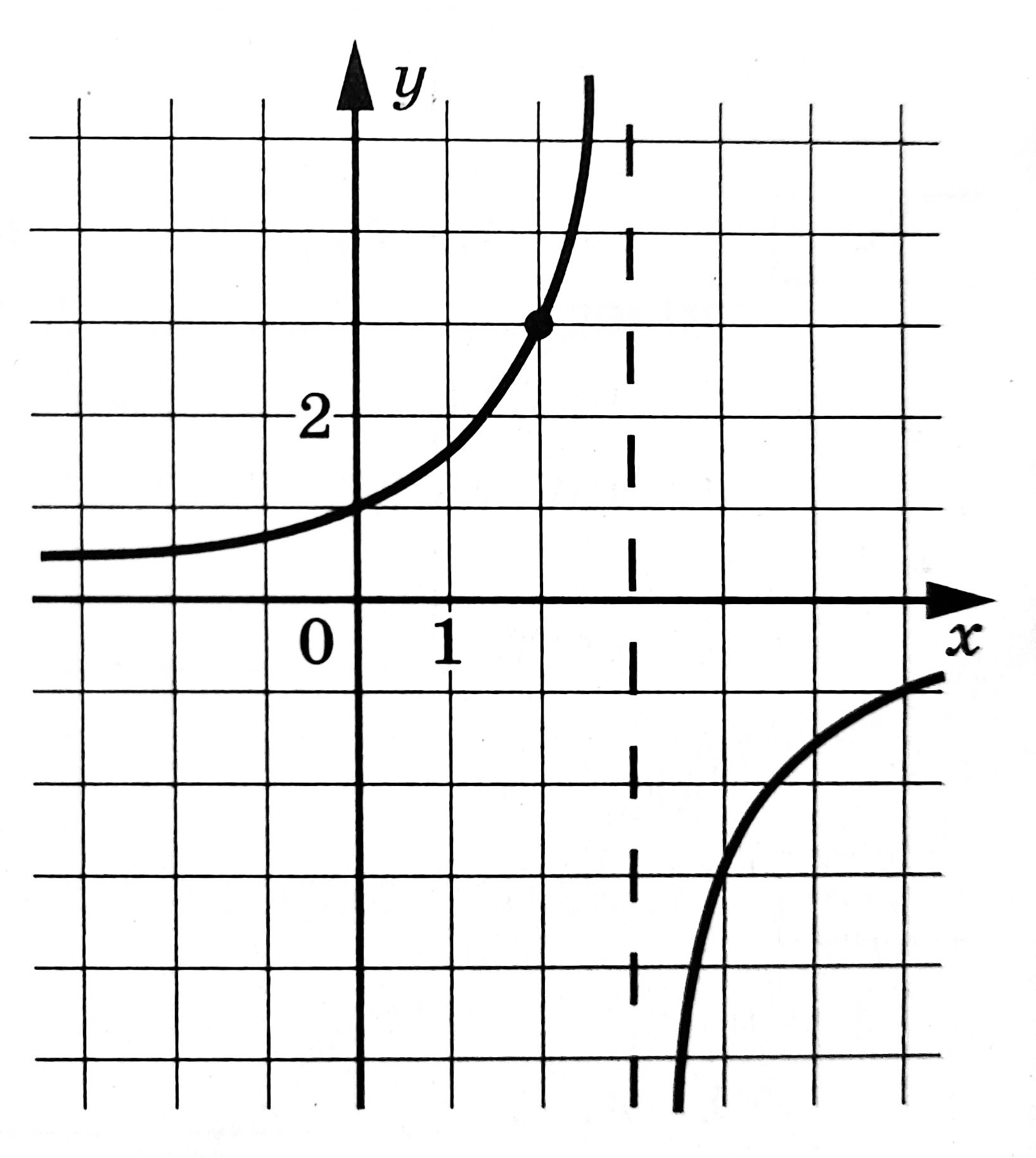
На рисунке изображён график функции \(f(x)=\dfrac{k}{x+a}\). Найдите \(f(18)\)

​

Найдите наибольшее значение функции \(y=(x+15)^2\cdot e^{-13-x}\) на отрезке [-14;-12]

а) Решите уравнение \(\cos^4\dfrac{x}4-\sin^4\dfrac{x}4=\sin\left(x-\dfrac{\pi}2\right)\)
​б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\pi;5\pi\right]\)

В правильной треугольной пирамиде SABC с основанием ABC точки D и E делят соответственно рёбра AC и SB так, что AD:DC=SE:EB=1:3. На продолжении ребра SC за точку S отмечена точка O. Прямые OD и OE пересекают рёбра AS и BC в точках P и F соответственно, причём CF=2FB.
a) Докажите, что отрезки DE и PF пересекаются.
б) Найдите отношение AP:AS.

Запишите ответ в виде несократимого отношения, например "4:13".

Решите неравенство \(3\cdot25^{1-\frac3{x}}-152\cdot15^{-\frac3{x}}+5\cdot3^{2-\frac6{x}}>0\)

В июле 2026 года планируется взять кредит в банке на некоторую сумму на 4 года. Условия его возврата таковы:
- каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
​- с февраля по июнь каждого года необходимо выплатить 324000 рублей.
​Какую сумму (в рублях) планируется взять в кредит, если он будет полностью погашен этими четырьмя платежами?

Окружность с центром в точке O вписана в ромб ABCD и касается его сторон AB, CD и AD соответственно в точках F, K и P.
a) Докажите, что прямая FP параллельна диагонали ромба BD.
б) Найдите площадь ромба ABCD, если известно, что FP=6 и PK=8.

Найдите все значения \(a\), при каждом из которых площадь фигуры, ограниченной линиями \(y=\dfrac{a}2x+a\) и \(y=a|x|-\left|\dfrac{a}2\right|\), будет больше 6, но не больше 12.

На координатной прямой отмечены целые числа. Митя играет в следующую игру: фишка стоит на отметке 0; Митя бросает игральный кубик и сдвигает фишку на выпавшее число очков вправо (положительное направление прямой), если выпадает чётное число очков, и влево (отрицательное направление прямой), если выпадает нечётное число очков. Через некоторое время Митя закончил игру.
a) Может ли фишка оказаться на отметке «0», если Митя 45 раз бросил кубик?
б) Известно, что чётное число очков выпадало столько же раз, сколько и нечётное число очков. Какое наименьшее число бросков кубика понадобится, чтобы фишка оказалась на отметке «-35»?
​в) Известно, что чётное число очков выпадало столько же раз, сколько и нечётное число очков. Какое наименьшее число бросков кубика понадобится, чтобы фишка оказалась на отметке «-40», если также известно, что при бросании кубика каждая грань выпадала хотя бы один раз, но любые две грани не выпадали одинаковое количество раз?

Введите ответ в форме строки "да;12;34". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.