36 вариантов ЕГЭ 2025
Меню курса
11 вариант ЕГЭ Ященко 2025
В треугольнике ABC угол C равен 90°, AB=5, sinA=0,28. Найдите AC.
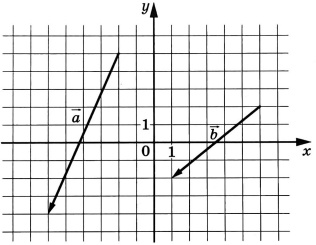
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение векторов \(\vec{a}\) и \(2\vec{b}\)
В цилиндрический сосуд налили 2100 см³ воды. Уровень жидкости оказался равным 20 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 5 см. Найдите объём детали? Ответ выразите в см³.
В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий третьим, окажется из Индии.
На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Найдите корень уравнения \(3^{\log_{27}(8x+4)}=4\)
Найдите значение выражения \(\left(8^5\right)^3:\left(4^2\right)^9\)
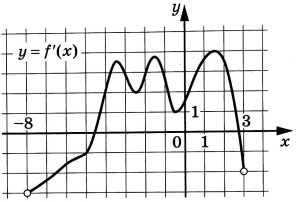
На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (-8;3). Найдите промежутки возрастания функции f(x). В ответ укажите сумму целых точек, входящих в эти промежутки.
В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону \(H(t)=H_0-\sqrt{2gH_0}kt+\dfrac{g}{2}k^2t^2\), где \(t\) - время в секундах, прошедшее с момента открытия крана, \(H_0=5\)м - начальная высота столба воды, \(k=\dfrac{1}{700}\) - отношение площадей поперечных сечений крана и бака, а \(g\) - ускорение свободного падения (считайте \(g=10\,м/с^2\)). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 621 литр она заполняет на 9 минут дольше, чем вторая труба заполняет резервуар объемом 486 литров?
Найдите наименьшее значение функции \(y=(x^2-10x+10)e^{2-x}\) на отрезке [-1;7]
а) Решите уравнение \(\sin x\cdot\cos2x-\sqrt3\cos^2x+\sin x=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}2;4\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
В основании прямой призмы ABCDA₁B₁C₁D₁ лежит параллелограмм ABCD. На рёбрах A₁B₁, B₁C₁ и BC отмечены точки M, K и N соответственно, причём B₁K:KC₁=1:3. Четырёхугольник AMKN – равнобедренная трапеция с основаниями 2 и 4.
а) Докажите, что точка N – середина ребра BC.
б) Найдите площадь трапеции AMKN, если объём призмы равен 24, а высота призмы равна 3.
Решите неравенство \(2^{-2\sqrt{x}}+32\cdot10^{2-\sqrt{x}}>2^{9-2\sqrt{x}}+625\cdot10^{-2-\sqrt{x}}\)
В июле 2027 года планируется взять кредит на десять лет в размере 1500 тыс. рублей. Условия возврата таковы:
- каждый январь долг будет возрастать на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
- в июле 2028, 2029, 2030, 2031 и 2032 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
- в июле 2033, 2034, 2035, 2036 и 2037 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2037 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 2400 тыс. рублей. Сколько рублей составит платёж в 2029 году?
Прямая, перпендикулярная стороне BC ромба ABCD, пересекает его диагональ AC в точке M, а диагональ BD в точке N, причём AM:MC=1:2, BN:ND=1:3.
а) Докажите, что прямая MN делит сторону ромба BC в отношении 1:4.
б) Найдите сторону ромба, если MN=√12.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}(xy-3x+9)\cdot\sqrt{y-3x+9}=0\\y=4x+a\end{cases}\) имеет ровно два различных решения.
В классе больше 10, но не больше 28 учащихся, а доля девочек не превышает 22%.
а) Может ли в этом классе быть 4 девочки?
б) Может ли доля девочек составить 30%, если в этот класс придёт новая девочка?
в) В этот класс пришла новая девочка. Доля девочек в классе составила целое число процентов. Какое наибольшее число процентов может составить доля девочек в классе?
Введите ответ в форме строки "да;нет;146". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.