5 вариант ЕГЭ Ященко 2025

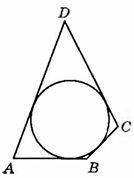
В четырехугольник ABCD вписана окружность, AB=10, BC=8 и CD=14. Найдите четвертую сторону четырехугольника.

​

Даны векторы \(\vec{a}(-3;-2)\) и \(\vec{b}(3;b_0)\). Найдите \(b_0\), если \(\vec{a}\cdot\vec{b}=0\)

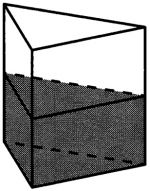
В сосуде, имеющем форму правильной треугольной призмы, уровень жидкости достигает 120 см. На какой высоте будет находится уровень жидкости, если её перелить в другой сосуд такой же формы, сторона основания которого в 4 раза больше, чем у первого? Ответ дайте в сантиметрах.

На олимпиаде по физике 250 участников собираются разместить в четырёх аудиториях: в трёх по 70 человек, а оставшихся - в запасной аудитории в другом корпусе. Найдите вероятность того, что случайно выбранный участник будет писать олимпиаду в запасной аудитории.

На двух линиях выпускают одинаковые лампы. Первая линия выпускает в три раза больше ламп, чем вторая, но вероятность брака на первой линии равна 0,1, а на второй - 0,06. Все лампы поступают на склад. Найдите вероятность того, что случайно выбранная лампа на складе окажется не бракованной.

Найдите корень уравнения \(4^{x-5}=8^{4x-2}\)

Найдите значение выражения \((1-\log_515)(1-\log_315)\)

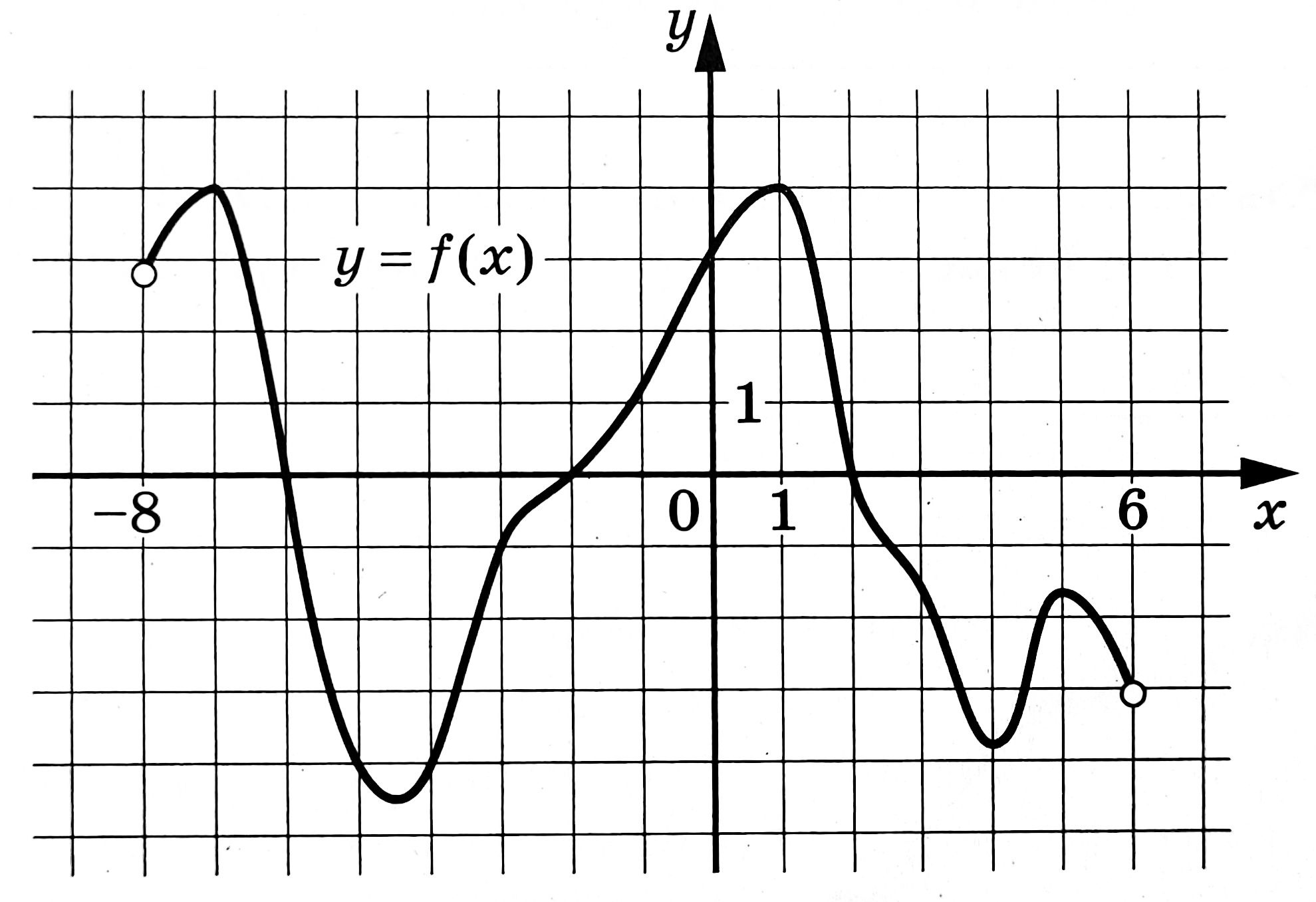
На рисунке изображён график функции y=f(x), определённой на интервале (-8;6). Определите количество целых точек, в которых производная функции f(x) отрицательна.

​

Два тела массой m=10 кг каждое движутся с одинаковой скоростью v=8 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле Q=mv²sin²α, где m — масса в килограммах, v — скорость в м/с. Найдите, под каким наименьшем углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 480 джоулей.

Из пункта А круговой трассы выехал велосипедист. Через 20 минут он еще не вернулся в пункт А, и из пункта А следом за ним отправился мотоциклист. Через 5 минут после отправления он догнал велосипедиста в первый раз, а еще через 46 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 46 км. Ответ дайте в км/ч.

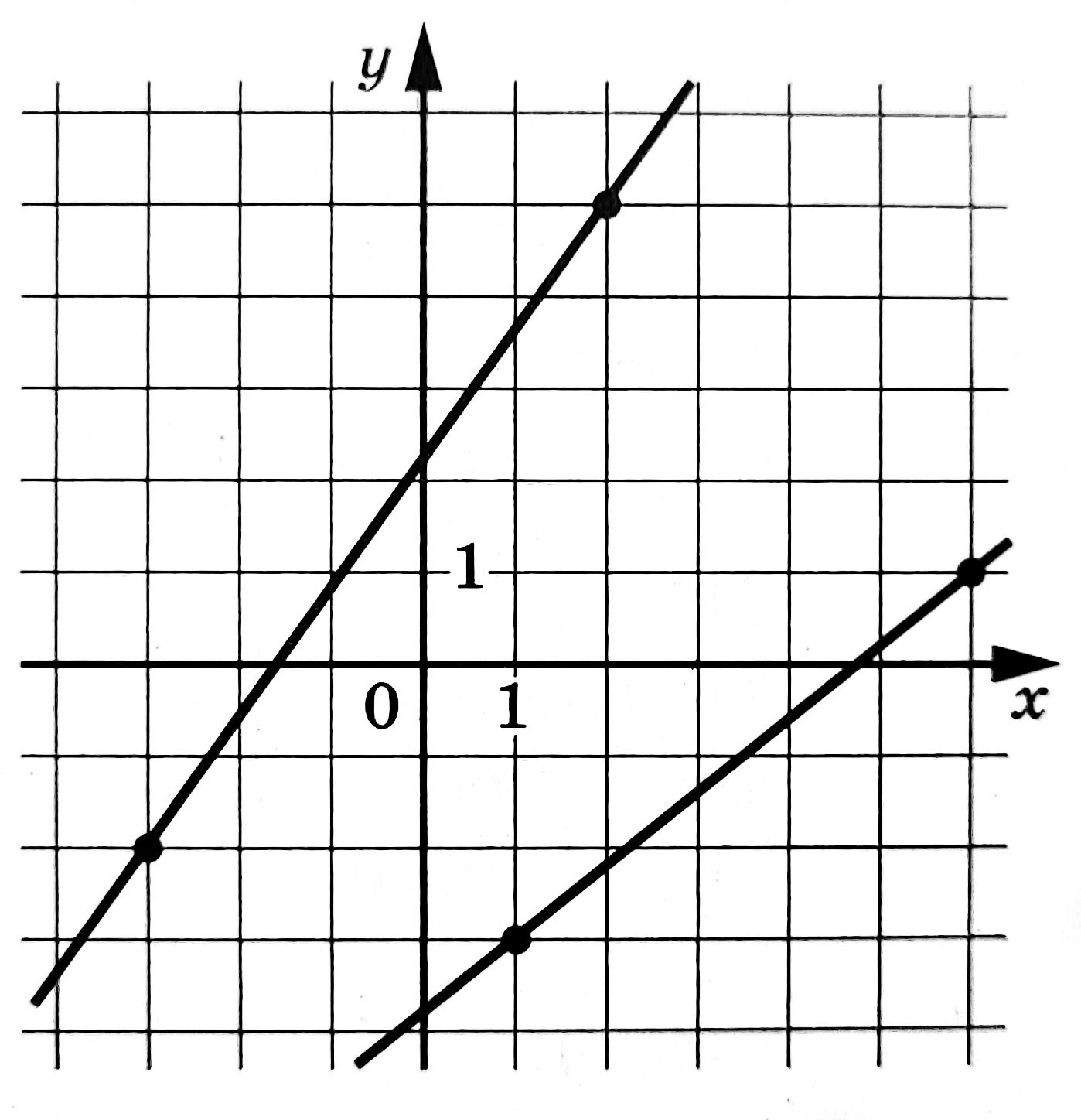
На рисунке изображены графики функций f(x)=kx+b, которые пересекаются в точке A(x₀;y₀). Найдите y₀.

Найдите точку минимума функции \(y=4x^{\frac32}-15x+3\)

а) Решите уравнение \(\log^2_{0{,}5}(x^2)-4\log_8(x^4)=1\)
б) Найдите все корни этого уравнения, принадлежащие отрезку [-0,9;2,9]

Основанием пирамиды SABCD является квадрат ABCD, ребро SA является высотой пирамиды. На рёбрах BC, CD и SC соответственно отмечены точки K, N и F так, что BK:KC=CN:ND=1:2, CF:FS=2:7.
а) Докажите, что плоскости ABC и FNK перпендикулярны.
6) Найдите объём пирамиды AFNK, если AB=AS=6.

Предприятие планирует 1 июня 2027 года взять в банке кредит на 2 года в размере 8400 тыс. рублей. Банк предложил предприятию два различных варианта погашения кредита, описание которых приведено в таблице.

На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для предприятия варианту погашения кредита?

В параллелограмме ABCD биссектриса угла BAD пересекает сторону BC в точке K, a продолжение стороны DC - в точке P; диагональ AC является биссектрисой угла KAD.
а) Докажите, что PC²=CD·PK.
6) Haйдите AC:AP, ecли BC:AB=2,5.

Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}(x+4)^2+(4-y)^2=0{,}1a^2-4(x+1)-4(y+1),\\|2x-3|-|4-y|=5\end{cases}\) имеет poвно два решения.

Каждый год в соревнованиях, состоящих из 10 этапов, участвует 10 спортсменов. По итогам каждого этапа один спортсмен занимает первое место, один спортсмен - второе и один - третье. В результате ежегодных соревнований каждый спортсмен занимает a первых, b вторых и c третьих мест. В зависимости от мест, занятых спортсменом на всех этапах (одного года), ему присваивается итоговый рейтинг соревнований.
В этом году по итогам 10 этапов каждому спортсмену присваивается 10a+4b+c очков; чем у спортсмена очков больше, тем рейтинг выше. Если количество очков у спортсменов совпадает, то рейтинги у них одинаковые.
​В прошлом году в таких же соревнованиях участвовали те же спортсмены. Но для подведения итогов соревнований рейтинги спортсменов определялись следующим образом: если у спортсмена-1 количество первых, вторых и третьих мест соответственно равно a₁, b₁ и c₁, а у спортсмена-2 – a₂, b₂ и c₂, то рейтинг спортсмена-1 был выше peйтинга спортсмена-2 в следующих случаях:
​- a₁> a₂,
- a₁=a₂ н b₁>b₂ ,
- a₁=a₂, b₁=b₂ и c₁>c₂.
​Ecли количество и первых, и вторых, и третьих мест у спортсменов совпадало, то рейтинги у них были одинаковые.
​a) В этом году по итогам соревнований у спортсменов нет совпадающих peйтингов. Если бы рейтинги определялись, как в прошлом году, то у спортсменов бы тоже не было совпадающих рейтингов. Может ли порядок рейтингов спортсменов этом году совпадать с порядком рейтингов прошлого года?
​б) По итогам соревнований этого года получилось, что у любых двух спортсменов нет одинаковых рейтингов. Какая наибольшая разница в очках может быть между двумя наименьшими рейтингами?
​в) Каждый год по результатам соревнований вычисляется средний балл Q для спортсменов, набравших хотя бы одно очко: отношение суммы всех набранных очков количеству спортсменов, набравших хотя бы одно очко. В следующем году планируется проводить аналогичные соревнования (10 этапов) с участием 10 спортсменов, где каждому из них будут присваиваться 10a+k₁b+k₂c очков. Организаторы обсуждают в данной формуле целые значения k₁ и k₂, такие, что 1≤k₂≤k₁≤9. Найдите все пары (k₁;k₂), при которых возможно получить наибольшее количество целых значений среднего балла Q.

Введите ответ в форме строки "да;51;(1;7);(2;3);(8;4)". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы, пары записаны в скобки без пробелов через ";", по возрастанию k₁