36 вариантов ЕГЭ 2025
Меню курса
30 вариант ЕГЭ Ященко 2025
Основания равнобедренной трапеции равны 45 и 14. Высота трапеции равна 9,3. Найдите тангенс острого угла.
Даны векторы \(\vec{a}(4;-6)\) и \(\vec{b}(-2;3)\). Известно, что \(|\vec{c}|=|\vec{a}|\), а векторы \(\vec{c}(x_c;y_c)\) и \(\vec{b}\) противоположно направленные. Найдите \(x_c+y_c\)
Прямоугольный параллелепипед описан около сферы радиуса 2,5. Найдите площадь его поверхности.
Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Найдите корень уравнения \(\sqrt{\dfrac{50}{5x+45}}=1\dfrac14\)
Найдите значение выражения \(2^{12\log_85}\)
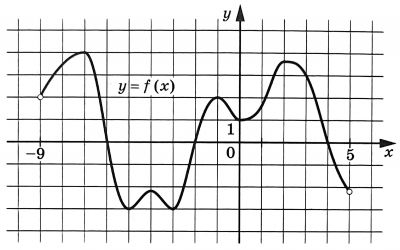
На рисунке изображен график функции y=f(x), определенной на интервале (-9;5). Найдите сумму точек экстремума функции f(x).
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа \(v\) вычисляется по формуле \(v=c\cdot\dfrac{f-f_0}{f+f_0}\), где \(c=1500\) м/с – скорость звука в воде, \(f_0\) – частота испускаемых импульсов, \(f\) – частота отраженного от дна сигнала, регистрируемая приемником (в МГц). Определите частоту отраженного сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Боря и Ваня могут покрасить забор за 10 часов. Ваня и Гриша могут покрасить этот же забор за 15 часов, а Гриша и Боря – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
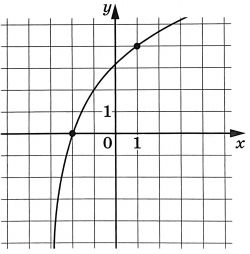
На рисунке изображен график функции \(f(x)=\log_a(x+3)\). Найдите значение \(x\), при котором \(f(x)=16\)
Найдите наименьшее значение функци \(y=e^{2x}-9e^x-3\) на отрезке [0;3].
а) Решите уравнение \(2\sin x\cdot\sin2x=2\cos x+\cos2x\)
б) Укажите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{5\pi}{2};-\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
Грань ABCD прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ является вписанной в основание конуса, а сечением конуса плоскостью A₁B₁C₁ является круг, вписанный в четырехугольник A₁B₁C₁D₁; AB=a, AA₁=√2a.
а) Высота конуса равна h. Докажите, что 4,5a< h< 5a.
б) Найдите угол между плоскостями ABC и SD₁C, где S – вершина конуса.
Решите неравенство \(\log_5x^2+4\log_{25}(6-2x)\geqslant\log_{\sqrt5}(x^2-4)+2\log_{0{,}2}(2-x)\)
В июле Анна планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Анне оформить кредит на следующих условиях:
– в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая – может быть разным для разных годов);
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором – 15, 10 и 20 процентов. Анна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей. В ответ запишите количество миллионов.
На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно. Около четырёхугольников AKND и BCNK также можно описать окружность. Косинус одного из углов четырёхугольника ABCD равен 0,2.
а) Докажите, что прямые KN и AD параллельны.
б) Найдите радиус окружности, описанной около четырёхугольника BCNK, если радиус окружности, описанной около четырёхугольника ABCD, равен 7, AK:KB=9:10, а BC< AD и BC=10.
Найдите все такие значения \(a\), при каждом из которых уравнение \(\sqrt{10x^2-19x-15}\cdot\log_3(7-(a-4)(x+2))=0\) имеет ровно два различных корня.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 7735.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из шести членов?
в) Какое наибольшее количество членов может быть в последовательности?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.