27 вариант ЕГЭ Ященко 2025

В треугольнике ABC известно, что AC=BC, высота AH=6√6, BH=3. Найдите cos∠BAC.

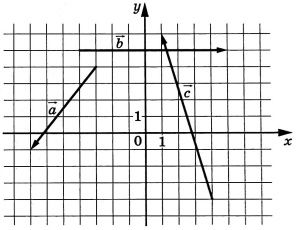
На координатной плоскости изображены векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\). Найдите длину вектора \(\vec{a}+\vec{b}-\vec{c}\)

​

Найдите объём многогранника, вершинами которого являются вершины B,C,A₁,C₁ правильной треугольной призмы ABCA₁B₁C₁, площадь основания которой равна 5, а боковое ребро равно 6.

В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Н. полетит вторым рейсом вертолёта.

Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 5. Какова вероятность, что для этого потребовалось два броска? Ответ округлите до сотых.

Найдите корень уравнения \(\left(\dfrac14\right)^{x+2}=256^x\)

Найдите значение выражения \(\log_{2{,}5}6\cdot\log_60{,}4\)

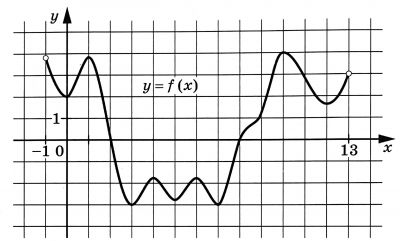
На рисунке изображен график функции y=f(x), определенной на интервале (-1;13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=-2.

​

Высота над землей подброшенного вверх мяча меняется по закону \(h(t)=1{,}4+11t-5t^2\), где \(h\) – высота в метрах, \(t\) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?

Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?

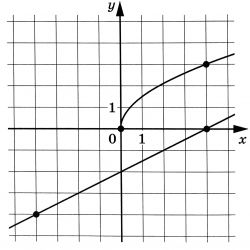
На рисунке изображены графики функций \(f(x)=a\sqrt{x}\) и \(g(x)=kx+b\), которые пересекаются в точке \(A(x_0;y_0)\). Найдите \(y_0\)

​

Найдите точку максимума функции \(y=(2x-1)\cos x-2\sin x+9\) принадлежащую промежутку \(\left(0;\dfrac{\pi}{2}\right)\).

а) Решите уравнение \(\log^2_2(4x^2)+3\log_{0{,}5}(8x)=1\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([0{,}15;1{,}5]\)

Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что M – середина SB.
б) Найдите расстояние между прямыми AC и DM, если высота пирамиды равна 6√3.

Решите неравенство \(\dfrac{\sqrt{x+4}\left(8-3^{2+x^2}\right)}{4^{x-1}-3}\leqslant0\)

15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей. В ответ запишите количество миллионов.

Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной из вершины C. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что I и J лежат на отрезке EF.
б) Найдите расстояние от точки C до прямой IJ, если AC=15, BC=20.

Найдите все значения \(a\), при каждом из которых оба уравнения \(a+\dfrac{x}2=|x|\) и \(a\sqrt2+x=\sqrt{2a\sqrt2x-x^2+12}\) имеют ровно 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.

Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 68?
б) Может ли n равняться 86?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.