36 вариантов ЕГЭ 2025
Меню курса
16 вариант ЕГЭ Ященко 2025
Найдите хорду, на которую опирается угол 135°, вписанный в окружность радиуса 3√2.
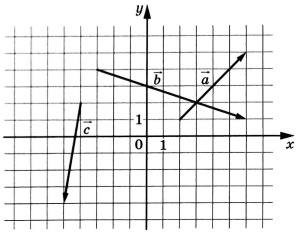
На координатной плоскости изображены векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\). Найдите длину вектора \(\vec{a}+\vec{b}+\vec{c}\)
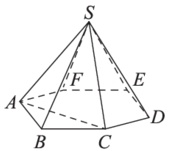
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 14. Найдите объём шестиугольной пирамиды.
Фабрика выпускает сумки. В среднем на 30 качественных сумок приходится 2 сумки, имеющие скрытые дефекты. Найдите вероятность того, что купленная в магазине сумка окажется с дефектами.
В коробке 6 синих, 12 красных и 7 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решите уравнение \(\log_2(x+5)=\log_4(1-x)\). Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Найдите значение выражения \(\dfrac{\sqrt[24]{a}\cdot\sqrt[48]{a}}{a\sqrt[16]{a}}\) при \(a=2{,}5\)
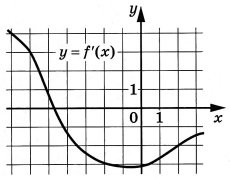
На рисунке изображен график y=f’(x) - производной функции y=f(x). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x+1 или совпадает с ней.
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём меняется по закону \(H(t)=at^2+bt+H_0\), где \(H_0=6{,}25\,м\) – начальный уровень воды, \(a=\dfrac1{49}\,м/мин^2\) и \(b=-\dfrac57\,м/мин\) – постоянные, \(t\) – время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ дайте в минутах.
От пристани A к пристани B, расстояние между которыми равно 192 км, отправился с постоянной скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью на 4 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч.
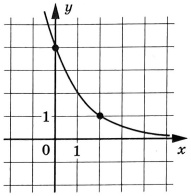
На рисунке изображён график функции \(f(x)=pa^x\). Найдите значение \(x\), при котором \(f(x)=32\)
Найдите точку максимума функции \(y=-\dfrac43x\sqrt{x}+7x+15\)
а) Решите уравнение \((2x^2-15x+18)\left(\sin x\cdot\sin\left(x-\dfrac{\pi}2\right)+0{,}25\right)=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{\pi}{2};2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. π/12+πn, n∈Z | 2. 5π/12+πn, n∈Z | 3. 7π/12+πn, n∈Z | 4. 11π/12+πn, n∈Z |
| 5. 1,5 | 6. 3 | 7. 4,5 | 8. 6 |
б)
| 9. 7π/12 | 10. 11π/12 | 11. 13π/12 | 12. 17π/12 |
| 13. 19π/12 | 14. 23π/3 | 15. 1,5 | 16. 3 |
| 17. 4,5 | 18. 6 |
На рёбрах AB и A₁C₁ правильной треугольной призмы ABCA₁B₁C₁ отметили соответственно точки T и K так, что AT:TB=1:2 и A₁K=KC₁. Через точки K и C параллельно прямой TA₁ проведена плоскость α.
а) Докажите, что точка пересечения плоскости α с ребром AB делит это ребро в отношении 2:1, считая от точки A.
б) Найдите площадь сечения призмы ABCA₁B₁C₁ плоскостью α, если AB=6√7, AA₁=3.
Решите неравенство \(\log_{0{,}2}^2(x+5)^4-4\log_{25}(x+5)^{12}\geqslant40\)
В августе 2027 года Алина планирует взять кредит в банке на 8 лет. Условия его возврата таковы:
- в январе 2028, 2029, 2030 и 2031 годов долг увеличивается на 15% от суммы долга на конец предыдущего года;
- в январе 2032, 2033, 2034 и 2035 годов долг увеличивается на 13% от суммы долга на конец предыдущего года;
- в период с февраля по июль необходимо выплатить часть долга;
- в августе каждого года действия кредита долг должен быть на одну и ту же сумму меньше долга на август предыдущего года;
- к августу 2035 года кредит должен быть полностью погашен.
Найдите сумму кредита (в млн рублей), если она на 1690 тыс. рублей меньше суммы общих выплат по кредиту.
В трапеции KLMN с основаниями KN и ML провели биссектрисы углов LKN и LMN, которые пересеклись в точке P. Через точку P параллельно прямой KN провели прямую, которая пересекла стороны LK и MN соответственно в точках A и B. При этом AB=KL.
а) Докажите, что трапеция KLMN равнобедренная.
б) Найдите cos∠LKN, если KP:PM=4:3, AP:PB=3:2.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}\left(\dfrac{|x-1|+|x+1|}2-7\right)^2+\left(\dfrac{|y-7|+|y+7|}2+1\right)^2=100\\y=ax+8\end{cases}\) имеет ровно два различных решения.
Среднее геометрическое \(k\) чисел \(p_1, p_2, ..., p_k\) вычисляется по формуле \(\sqrt[k]{p_1\cdot p_2\cdot...\cdot p_k}\).
а) Может ли среднее геометрическое трёх различных двузначных чисел быть равно 36?
б) Найдите наименьшее возможное целое значение среднего геометрического четырёх различных двузначных чисел.
в) Найдите наименьшее возможное целое значение среднего геометрического шести различных двузначных чисел.
Введите ответ в форме строки "да;45;14". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.